Cet exemple montre :
- le circuit réluctant permettant de modéliser l’actionneur linéaire
- l’optimisation mono-objectif (minimisation de la masse)
- le post-processing du résultat d’optimisation
Modélisation
L’objectif de la modélisation est de mettre en place le circuit et les équations permettant de calculer la masse et la force dans l’entrefer sur le noyau mobile du dispositif.
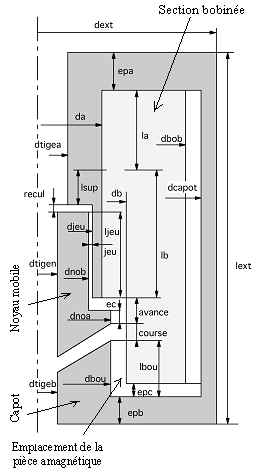
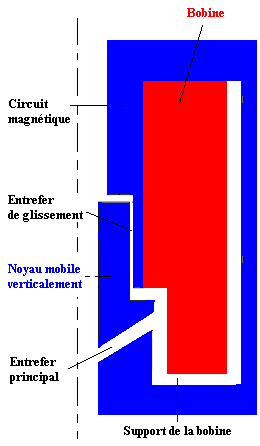
Les paramètres d’entrée
| alpha |
Angle d’inclinaison de l’entrefer [rad] |
| avance |
Dimension géométrique [mm] |
| coursea |
Dimension géométrique [mm] |
| coursez |
Dimension géométrique [mm] |
| da |
Dimension géométrique [mm] |
| db |
Dimension géométrique [mm] |
| dbou |
Dimension géométrique [mm] |
| dcapot |
Dimension géométrique [mm] |
| dens |
Densité de courant dans la bobine [A/mm2] |
| dext |
Diamètre extérieur [mm] |
| dtidgeb |
Dimension géométrique [mm] |
| dtidgen |
Dimension géométrique [mm] |
| ec |
Dimension géométrique [mm] |
| epa |
Dimension géométrique [mm] |
| epb |
Dimension géométrique [mm] |
| epc |
Dimension géométrique [mm] |
| jeu |
Dimension géométrique [mm] |
| jeubob |
Dimension géométrique [mm] |
| kbob |
Coefficient de remplissage du bobinage [-] |
| lbou |
Dimension géométrique [mm] |
| ljeu |
Dimension géométrique [mm] |
| longueu |
Longueur du dispositif [mm] |
| lsup |
Dimension géométrique [mm] |
| recul |
Dimension géométrique [mm] |
Le circuit
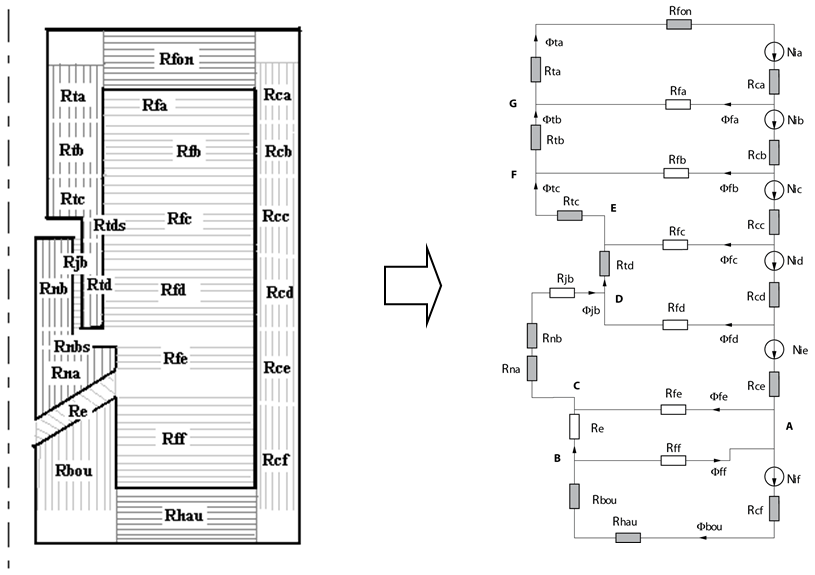
Les paramètres des composants du circuit
- Rfon:
- type: SATREL
- L = dcapot
- S = Sfon
- Rca:
- type: SATREL
- L = (la+epa)/2.0
- S = Scapot
- Rcb:
- type: SATREL
- L = la/2.0
- S = Scapot
- Rcc, Rcd:
- type: SATREL
- L = lb/2.0
- S = Scapot
- Rce:
- type: SATREL
- L = lc-lbou
- S = Scapot
- Rcf:
- type: SATREL
- L = lbou+epb/2.0
- S = Scapot
- Rhau:
- type: SATREL
- L = dcapot
- S = Shau
- Rbou:
- type: SATREL
- L = lbou+epb/2.0
- S = Sbou
- Rna:
- type: SATREL
- L = ec
- S = Sna
- Rnb:
- type: SATREL
- L = recul+coursez-coursea
- S = Snb
- Rtd:
- type: SATREL
- L = recul+coursez-coursea
- S = Std
- Rtc:
- type: SATREL
- L = lsup
- S = Sta
- Rtb:
- type: SATREL
- L = la/2.0
- S = Sta
- Rta:
- type: SATREL
- L = (la+epa)/2.0
- S = Sta
- Rfa, Rfb:
- type: AIRREL
- L = 0.5*log(dcapot/da)*da
- S = pi*da*(la/2.0)
- Rfc, Rfd:
- type: AIRREL
- L = 0.5*log(dcapot/da)*da
- S = pi*da*(lb/2.0)
- Rfe:
- type: AIRREL
- L = 0.5*log(dcapot/dnoa)*dnoa
- S = pi*dnoa*ec
- Rff:
- type: AIRREL
- L = 0.5*log(dcapot/dnoa)*dnoa
- S = pi*dbou*(lbou-epc)
- Rjb:
- type: AIRREL
- L = jeu
- S = Sjeu
- Re:
- type: INCLINED_AIRREL
- L = coursea
- a = avance/2.0
- d_ext = dnoa
- d_int = dtigen
- alpha = alpha
- Nia:
- type: JS_SRC
- J = dens
- S = ((dbob-da)/2.0)*(la/4.0)
- Nib:
- type: JS_SRC
- J = dens
- S =((dbob-da)/2.0)*(la/2.0)
- Nic:
- type: JS_SRC
- J = dens
- S =((dbob-da)/2.0)*((la+lb)/4.0)
- Nid:
- type: JS_SRC
- J = dens
- S = ((dbob-da)/2.0)*(lb/2.0)
- Nie:
- type: JS_SRC
- J = dens
- S = ((dbob-db)/2.0)*(lc-((lbou-epc)/2.0))+((dbob-da)/2.0)*(lb/4.0)
- Nif:
- type: JS_SRC
- J = dens
- S = ((dbob-db)/2.0)*((lbou-epc)/2.0)
- Le matériau féromagnetique utilisé a les caractéristiques suivantes (s’applique à tous les composants de type SATREL):
- a = 0.25
- alpha = 1.5
- beta = 1.5
- freq = 0.0
- Js = 2.1
- Kc = 4.98e-5
- Ke = 6.31e-4
- Kh = 0.0187
- mur = 800.0
- vol_mass = 7800.0
Les équations
/*
Actionneur lineaire.
Modèle issu de:
Christian Chillet and Jean-Yves Voyant - Design-Oriented Analytical Study of a
Linear Electromagnetic Actuator by Means of a Reluctance Network,
IEEE TRANSACTIONS ON MAGNETICS, VOL. 37, NO. 4, JULY 2001
*/
/*Calcul des surfaces des tubes des flux*/
Scapot=(pi/4.0)*(dext*dext-dcapot*dcapot);
Sfon= (pi*da*epa + pi*dcapot*epa)/2;
Sta=(pi/4.0)*(da*da-dtigea*dtigea);
Std=(pi/4.0)*(da*da-djeu*djeu);
Sjeu=pi*(dnob+jeu)*(ljeu-coursez+coursea);
Snb=(pi/4.0)*(dnob*dnob-dtigen*dtigen);
Sna=(pi/4.0)*(dnoa*dnoa-dtigen*dtigen);
Sbou=(pi/4.0)*(dbou*dbou-dtigeb*dtigeb);
Shau=(pi*dbou*epb + pi*dcapot*epb)/2;
/*Calcul de la masse*/
mvfer=7860;//masse volumique du fer
mvcui=8900;//masse volumique du cuivre
volbob=pi/4*(pow(dbob,2)*(la+lb+lc)-pow(da,2)*(la+lb)-pow(db,2)*lc); //volume bobinage
volfer=pi/4*(pow(dext,2)*longueu-pow(dcapot,2)*(la+lb+lc)+(pow(da,2)-pow(dtigea,2))*
(la+lsup)+pow(dbou,2)*((lb+lc-lsup)-coursez));//volume fer
massefe=mvfer*volfer*1e-9;//masse fer
massebo=mvcui*volbob*1e-9*kbob;//masse bobinage
masse=massefe+massebo;// masse totale
/*Force dans l'entrefer incliné*/
force=(pow((Re.flux/(Re.Setot*1e-6)),2)*Re.Sae*1e-6*cos(alpha*pi/180))/(2*mu0);
/*Géométrie à contraindre*/
dbob=dcapot-jeubob*2;
dnoa=dbou;
dnob=dnoa/sqrt(2);
djeu=dnob+2*jeu;
dtigea=djeu;
lc=lbou+avance+coursez-epc;
lb=ljeu+recul+lsup;
la=longueu-epa-lb-lc-epc-epb;
ecapot=(dext-dcapot)/2;
eda=(da-djeu)/2;
edb=(db-dbou)/2;
L’optimisation
Le scénario d’optimisation est le suivant :
- Trouver la valeur optimale de :
- Diamètre extérieur (dext)
- Longueur (Longueu)
- Et les dimensions suivantes: da, db, dbou, dcapot, epa, epb
- Tel que :
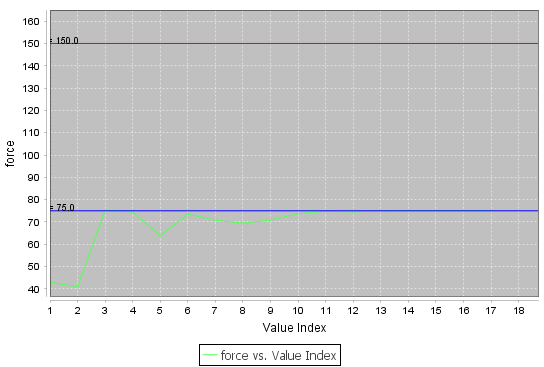
- La force dans l’entrefer soit supérieure à 75N (force)
- Épaisseur du capot soit compris entre 1.5 et 1.8 (ecapot)
- Épaisseur eda soit inférieur à 5.0 (eda)
- Longueur la soit inférieur à 10.0 (la)
- Longueur lb soit inférieur à 30.0 (lb)
- La masse soit minimale (masse)
- Pour une valeur imposée de:
- Épaisseur edb à 1.0
- Toutes les autres variables d’entrée
Le cahier des charges
/*Les intervalles de libertés d’optimisation*/
da - Interval = [20.0..30.0] - valeur initiale = 24.0
db - Interval = [22.0..35.0] - valeur initiale = 27.0
dbou - Interval = [20.0..32.0] - valeur initiale = 26.0
dcapot - Interval = [50.0..65.0] - valeur initiale = 55.0
dext - Interval = [50.0..76.0] - valeur initiale = 60.0
epa - Interval = [2.0..7.0] - valeur initiale = 5.0
epb - Interval = [2.0..7.0] - valeur initiale = 5.0
Longueu - Interval = [45.0..70.0] - valeur initiale = 50.0
/*Les variables d'entrée imposées*/
alpha - Fixe - valeur = 45.0
avance - Fixe - valeur = 3.0
coursea - Fixe - valeur = 10.0
coursez - Fixe - valeur = 10.0
dens - Fixe - valeur = 5.0
dtigeb - Fixe - valeur = 5.0
dtigen - Fixe - valeur = 5.0
ec - Fixe - valeur = 1.5
epc - Fixe - valeur = 1.0
jeu - Fixe - valeur = 0.05
jeubob - Fixe - valeur = 0.2
kbob - Fixe - valeur = 0.45
lbob - Fixe - valeur = 10.0
ljeu - Fixe - valeur = 14.5
lsup - Fixe - valeur = 1.0
recul - Fixe - valeur = 0.5
/*Les contraintes sur les sortie*/
masse - Minimize - valuer = 1.0 - weight = 1.0
force - Interval = [75.0..150.0]
ecapot - Interval = [1.5..1.8]
eda - Interval = [0.0..5.0]
la - Interval = [1.0..10.0]
lb - Interval = [1.0..30.0]
edb - Fixed = 1.0
/*L'optimiseur*/
Optimizer = SQP
Optimizer.Precision = 1.0E-5
Optimizer.Max Iteration = 100
Le résultat d’optimisation
/*Les valeurs d'entrée trouvées*/
da - valeur initiale = 24.0 - valeur trouvée = 25.66
db - valeur initiale = 27.0 - valeur trouvée = 26.66
dbou - valeur initiale = 26.0 - valeur trouvée = 24.66
dcapot - valeur initiale = 55.0 - valeur trouvée = 64.09
dext - valeur initiale = 60.0 - valeur trouvée = 67.09
epa - valeur initiale = 5.0 - valeur trouvée = 2.45
epb - valeur initiale = 5.0 - valeur trouvée = 2.13
longueu - valeur initiale = 50.0 - valeur trouvée = 45.0 (limite min)
/*Les valeurs de sorties trouvées*/
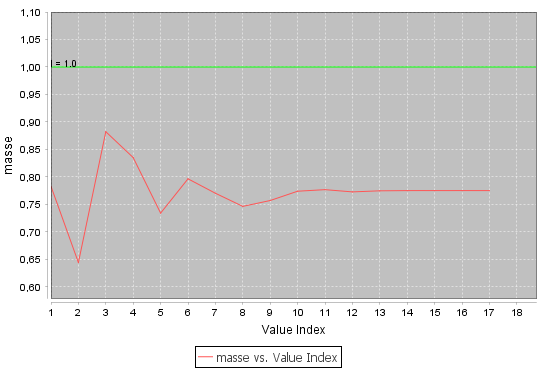
masse - valeur = 0.78 (Minimisée)
force - valeur = 74.99 (limite min)
ecapot - valeur = 1.5 (limite max)
eda - valeur = 4.06
la - valeur = 1.41
lb - valeur = 16.0
edb - valeur = 1.0 (valuer imposée)
Le post-processing
Le post-processeur de Cades peut servir pour montrer l’évolution de la fonction objectif à travers d’itérations d’optimisation :