Cet exemple montre :
- les équations permettant de calculer le rendement du dispositif
- l’optimisation mono-objectif (minimisation de l’encombrement)
- le post-processing du résultat d’optimisation
- Optimisation pareto (encombrement vs. rendement)
Modélisation
L’objectif de la modélisation est de mettre en place les équations d’un convertisseur AC/DC en fonction de ses grandeurs caractéristiques (tensions d’entrée/sortie, puissance, rendement).
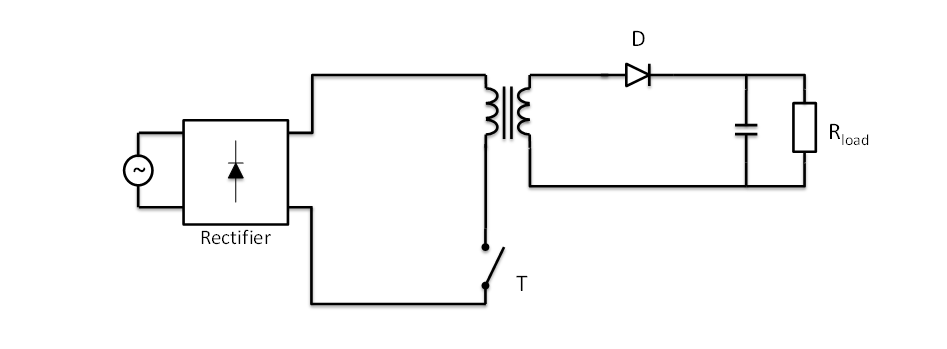
Le schéma du circuit est présentée en dessous. Le circuit de commande n’est pas pris en compte dans cet exemple.
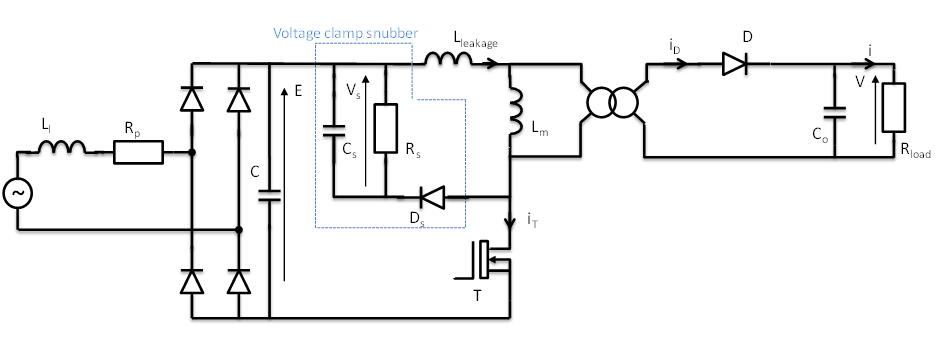
Les paramètres d’entrée
| e |
Entrefer du transformateur [m] |
| f |
Fréquence de hachage [Hz] |
| m |
Le rapport de transformation du transformateur [-] |
| Bmax |
L’induction maximale dans le noyau du transformateur [T] |
| d1 |
Le diamètre du fil de l’enroulement primaire [mm2] |
| d2 |
Le diamètre du fil de l’enroulement secondaire[mm2] |
| delta1 |
Densité du courant dans l’enroulement primaire [A/m2] |
| delta2 |
Densité du courant dans l’enroulement secondaire[A/m2] |
| deltaV_percent |
Distorsion admissible de la tension DC en sortie[%] |
| E |
Tension de sortie du redresseur[V] |
| I |
Courant en sortie[A] |
| k1 |
Coefficient de remplissage de l’enroulement primaire[-] |
| k2 |
Coefficient de remplissage de l’enroulement secondaire[-] |
| RD_on |
Résistance de la diode[ohm] |
| RT_on |
La résistance dynamique du transistor[ohm] |
| toff |
Décalage d’ouverture du transistor [s] |
| V |
Tension de sortie [V] |
| VD_reverse |
Tension de la diode [V] |
| VT_peak |
Tension admissible dans le transistor [V] |
| kp |
Paramètre de calcul de pertes fer (formulation Steinmetz) [-] |
| xp |
Paramètre de calcul de pertes fer (formulation Steinmetz) [-] |
| yp |
Paramètre de calcul de pertes fer (formulation Steinmetz) [-] |
Les équations
/*
Convertisseur Flyback
Fichier flyback.sml
Modele de dimensionnement d'un convertisseur flyback.
Réferénces:
Jean Paul FERRIEUX, François FOREST - Alimentations à découpage,
convertisseurs à résonance 3e édition, Dunod, Paris, 1999 ISBN 2100041371
Chérif LAROUCI. Conception et optimisation de convertisseurs statiques
pour l’électronique de puissance. Application aux structures à absorption
sinusoïdale. Thèse INPG LEG soutenue le 13 mai 2002.
Ludovic JOURDAN. Stratégie de pré dimensionnement de convertisseurs
statiques. Application à une alimentation 42V-14V réversible pour
l’automobile. Thèse UJF LEG soutenue le 15 juillet 2002.
*/
intern mu0;
mu0 = 4*pi*1e-7;
/*Ouput power*/
P = V*I;
/*Cyclic ratio*/
alpha = sqrt((2*Lm*V*I*f)/pow(E,2));
beta = alpha * (1.0 + E/(m*V));
/*Magnetizing inductance (at continuous & discontinuous conduction limit)*/
Lm = pow((E*m*V),2)/(2*f*P*pow((E+m*V),2));
/*Transistor data*/
IT = E*alpha/(Lm*f);
IT_rms = IT*sqrt(alpha/3);
IT_average = E*pow(alpha,2)/(2*Lm*f);
/*Diode data*/
ID = E*alpha*m/(Lm*f);
ID_rms = sqrt(pow(ID,2)*(beta-alpha)+(pow((pow(m,2)*V/Lm),2))*
pow((beta-alpha),3)/(3*pow(f,2))-2*ID*pow(m,2)*V*pow((beta-alpha),2)/(2*Lm*f));
/*Diode max current*/
IDmax = ( (V*I/(E*V*m/((V*m)+E))) + (E*m*V/(((V*m)+E)*2*Lm*f)) ) * m;
/*Transformer data*/
Aen = Lm*IT/Bmax;
Sfn = IT_rms*k1/(delta1*1e6) + ID_rms*k2/(m*(delta2*1e6));
AeSf = Aen*Sfn;
transformer_volume = 3e11*AeSf + 2772.3;
/*Leakage inductance estimation*/
L_leakage = Lm * 0.03;
/*Windings*/
n1 = sqrt((Lm*e)/(mu0*Aen));
n2 = n1/m;
/*Copper areas*/
A1 = IT_rms/(delta1*1e6);
A2 = ID_rms/(delta2*1e6);
A_copper = n1*k1*A1 + n2*k2*A2;
A_copper2 = pi*n1*k1*(pow(d1,2))/4+2*pi*n2*k2*(pow(d2,2))/4;
/*Voltage Clamp Snubber*/
Vs = VT_peak - E;
Rs = 2*Vs*(Vs-V/m)/(f*L_leakage*pow(IT, 2.0));
Cs = 10/(Rs*f);
VCS_losses = pow(Vs, 2.0)/Rs;
/*Output voltage smooth capacitor*/
Co = I/(deltaV_percent*V*f);
Co_volume = 1872.0*Co*1e6 + 250.0; //(400V series : mm^3 , Co in uF)
/*Rectifier voltage smooth capacitor*/
intern delatE_percent;
delatE_percent = 2.0;
C = IT_rms/(delatE_percent*E*50.0);
C_volume = 1872.0*C*1e6 + 250.0; //(400V series : mm^3 , C in uF)
/*Transistor commutation losses*/
Commutation_losses = (E+(V/m)+Vs)*E*alpha*toff/(2*Lm);
/*Transistor conduction losses*/
Conduction_losses_T = RT_on*pow(IT_rms,2);
/*Diode conduction losses*/
Conduction_losses_D = VD_reverse*I + RD_on*pow(ID_rms,2);
/*Transformer core losses*/
Core_losses = Kp2*pow(f,xp2)*pow(Bmax,yp2)*transformer_volume*1e-6;
/*Energetic balance*/
P_losses = Core_losses + Commutation_losses + Conduction_losses_T + Conduction_losses_D + VCS_losses;
/*Efficiency*/
Efficiency = P / (P + P_losses);
/*Total Volume (cm3)*/
Volume = transformer_volume + Co_volume + C_volume;
L’optimisation
Le scénario d’optimisation est le suivant :
- Trouver la valeur optimale de :
- L’entrefer du transformateur (e)
- La fréquence de hachage (f)
- Le rapport de transformation (m)
- Tel que :
- Le rendement soit supérieur à 0.85 (Efficiency)
- Le courant dans la diode soit inférieur à 14.0A (IDmax)
- Le volume du transformateur soit minimal (transformer_volume)
- Pour une valeur imposée de toutes les autres variables d’entrée
Le cahier des charges
/*Les intervalles de libertés d’optimisation*/
e - Interval = [2.0e-4..0.0015] - valeur initiale = 5.0e-4
m - Interval = [1.0..10.0] - valeur initiale = 1.0
f - Interval = [25000..100000] - valeur initiale = 50000
/*Les variables imposées*/
Bmax - Fixe - valeur = 0.2
d1 - Fixe - valeur = 0.4
d2 - Fixe - valeur = 0.8
delta1 - Fixe - valeur = 4.0
delta2 - Fixe - valeur = 4.0
deltaV_percent - Fixe - valeur = 2.0
E - Fixe - valeur = 325.0
I - Fixe - valeur = 4.5
k1 - Fixe - valeur = 3.0
k2 - Fixe - valeur = 3.0
kp2 - Fixe - valeur = 0.035
RT_on - Fixe - valeur = 4.0
toff - Fixe - valeur = 3.2e-8
V - Fixe - valeur = 20.0
VD_reverse - Fixe - valeur = 0.8
VT_peak - Fixe - valeur = 400.0
xp2 - Fixe - valeur = 1.1
yp2 - Fixe - valeur = 2.63
RD_on - Fixe - valeur = 0.1
/*Les contraintes sur les sortie*/
transformer_volume - Minimize - valuer = 3822.5 - weight = 1.0
Efficiency - Interval = [0.85..1.0]
IDmax - Interval = [0.0..14.0]
/*L'optimiseur*/
Optimizer = SQP
Optimizer.Precision = 1.0E-5
Optimizer.Max Iteration = 100
Le résultat d’optimisation
/*Les valeurs d'entrée trouvées*/
e - valeur initiale = 5.0e-4 - valeur trouvée = 5.0e-4
f - valeur initiale = 1.0 - valeur trouvée = 2.67
m - valeur initiale = 45e5 - valeur trouvée = 18.5e6
/*Les valeurs de sorties trouvées*/
transformer_volume - valeur = 4295.19 (Minimisée)
Efficiency - valeur = 0.85 (limite min)
IDmax - valeur = 10.48
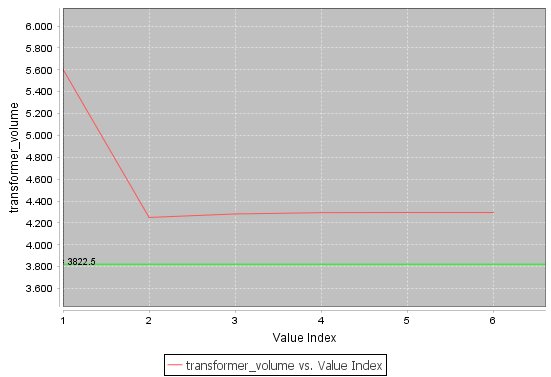
Le post-processing
Le post-processeur de Cades peut servir pour montrer l’évolution de la fonction objectif à travers d’itérations d’optimisation :
Optimisation pareto
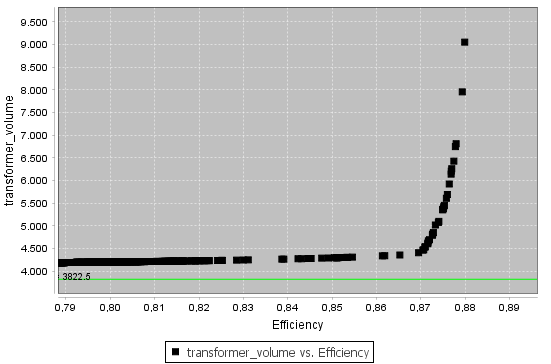
Pour obtenir le front pareto (taransformer_volume vs. rendement), il faut utiliser le cahier des charges suivant:
/*Les intervales de libertés d’optimisation*/
e - Interval = [2.0e-4..0.0015] - valuer initiale = 5.0e-4
m - Interval = [1.0..10.0] - valuer initiale = 1.0
f - Interval = [25000..100000] - valuer initiale = 50000
/*Les variables imposées*/
Bmax - Fixe - valeur = 0.2
d1 - Fixe - valeur = 0.4
d2 - Fixe - valeur = 0.8
delta1 - Fixe - valeur = 4.0
delta2 - Fixe - valeur = 4.0
deltaV_percent - Fixe - valeur = 2.0
E - Fixe - valeur = 325.0
I - Fixe - valeur = 4.5
k1 - Fixe - valeur = 3.0
k2 - Fixe - valeur = 3.0
kp2 - Fixe - valeur = 0.035
RT_on - Fixe - valeur = 4.0
toff - Fixe - valeur = 3.2e-8
V - Fixe - valeur = 20.0
VD_reverse - Fixe - valeur = 0.8
VT_peak - Fixe - valeur = 400.0
xp2 - Fixe - valeur = 1.1
yp2 - Fixe - valeur = 2.63
RD_on - Fixe - valeur = 0.1
/*Les contraintes sur les sortie*/
transformer_volume - Minimize - valuer = 3822.5 - weight = 1.0
Efficiency - Maximize - valuer = 1.0 - weight = 1.0
IDmax - Interval = [0.0..14.0]
/*L'optimiseur*/
Optimizer = NSGA2
L’information du front pareto se trouve dans
ce fichier des résultats. Il a l’allure suivante, montrant que pour des rendements supérieurs, il faut payer exponentiellement en volume: