Alternateur à griffes

Cet exemple montre :

1. les équations permettant de calculer la masse, le rendement et la puissance électrique l’alternateur
2. l’optimisation mono-objectif (minimisation de la masse)
3. le post-processing du résultat d’optimisation

Modélisation

L’objectif de la modélisation est de mettre en place les équations d’un alternateur à griffes permettant de résoudre le circuit équivalent magnétique et électrique et de calculer le rendement et la puissance du dispositif.

Les paramètres d’entrée

correction_pertes

delta

duty_cycle

fils_en_parallele

gamma

h_chanf

h_pied

h_semelle

K_aero

k_eddy

k_hyst

K_meca

l_chanf

L_tetes_bobines

M_sup

M_v_cu

M_v_fer

mu_r_dent

N

n_couches

N_phases

Nepp

p

Ra

Rd

rho_0_cu

rho_fer_griffe

rho_fer_stator

steinmetz

T_cu_rotor

T_cu_stator

Ub

Vbb

Vd

Vr

ep

h_bec

h_plateau

hd

Id

Iq

l_base_griffe

l_bout_griffe

largeur_dent

ln

lstator

N_cond_par_encoche

Nex

ouv_encoche

psi1

psi10

psi2

psi3

psi4

psi5

psi6

psi7

psi8

psi9

R_ext_rotor

R_ext_stator

R_int_stator

Rn

S_fil_rotor

S_fil_stator

Les équations du modèle principal

       

/***************************************************
Alternateur à griffes
alternateur_griffes1.sml		
      | Dimensionnement d'un alternateur à griffes |
      | (sans aimants permanents )		   |	
      |	Modele v2.1                                |
      |	Calcul sur un seul point de fonctionnement | 
      | Auteur : Laurent ALBERT                    |
      | Date : 27 / 04 / 2004                      |
      **********************************************
References:

Méthodes, modèles et outils en vue du dimensionnement et de l’optimisation des alternateurs pour applications automobiles ", these de l'Institut Polytechnique de Grenoble, 13 juillet 2004
https://tel.archives-ouvertes.fr/tel-00007091/

"Sizing of automotive claw-pole alternator based on analytical modeling"
L. ALBERT, C. CHILLET, A. JAROSZ, J. ROUSSEAU, F. WURTZ, ELECTROMOTION, vol. 12, 2005, Number 2 – 3, April - September 2005, pp. 118-124

"Analytic modelling of automotive claw-pole alternator for design and constrained optimisation" L. ALBERT, C. CHILLET, A. JAROSZ, F. WURTZ, European conference on Power Electronics and Applications (EPE’2003), Toulouse, France, 2-4 September 2003

*/


import org.gu.vesta:benchmark.website.java.ExternFunction:1.0;

/* Constantes du probleme et fonctions hyperboliques */
mu0=4*pi*pow(10,-7);

/* -----------------------------------------
Calculs des parametres intermediaires 
----------------------------------------- */

/* Parametres electriques deduits */
N_encoches=2*p*N_phases*Nepp;
N_spires_par_phase=N_cond_par_encoche*N_encoches/(2*N_phases);

/* Parametres geometriques deduits */
entrefer=R_int_stator-R_ext_rotor;
l_fond_encoche=(2*pi*(R_int_stator+hd)/N_encoches)-largeur_dent;
h_culasse=R_ext_stator-R_int_stator-hd;
pas_dentaire=2*pi*R_int_stator/N_encoches;
pas_polaire=pas_dentaire*N_encoches/(2*p);
beta=atan(2*ln/(l_base_griffe-l_bout_griffe));
dgg=sin(beta)*(2*pi*R_ext_rotor-p*(l_base_griffe+l_bout_griffe))/(2*p);
ecart_longueur=abs(lstator-ln);
h_base_griffe=R_ext_rotor-(Rn+h_plateau);
h_base_bec=h_base_griffe-h_bec;
xi=atan(h_base_bec/ln);
contrainte_trapeze=l_base_griffe-l_bout_griffe;
rdm_griffe=ln/h_base_griffe;

/* Calcul des parametres electriques */

/* Inductance de fuite */
Kf=mu0*pow(N_cond_par_encoche,2)*N_encoches*lstator/N_phases;
l_enc=Kf*((hd-h_pied)/(3*l_fond_encoche)+(h_pied-h_semelle)*log(l_fond_encoche/ouv_encoche)/(l_fond_encoche-ouv_encoche)+h_semelle/ouv_encoche);
l_zz=Kf*pow(pas_dentaire-ouv_encoche,2)/(8*entrefer*pas_dentaire);
l_tb=mu0*3*pow(N_spires_par_phase,2)*2*R_int_stator*0.6/pow(p,2);
Lf=(l_enc+l_zz+l_tb)/pow(3,delta);

/* Coefficient de correction des amperes tours d'induit */
Kri=6*(cos(p*l_bout_griffe/(2*R_ext_rotor))-cos(p*l_base_griffe/(2*R_ext_rotor)))
    /(pi*(l_base_griffe/(2*R_ext_rotor)-l_bout_griffe/(2*R_ext_rotor))*(l_base_griffe/(2*R_ext_rotor)+l_bout_griffe/(2*R_ext_rotor))*pow(p,2));

/* Inductance transversale */
S_entrefer=(pas_polaire-dgg*sin(beta))*lstator*(1-ouv_encoche/pas_dentaire);
Lq=mu0*pow(N_cond_par_encoche,2)*N_encoches*S_entrefer/(N_phases*4*entrefer)/pow(3,delta);

/* Resistance de l'enroulement statorique */
function rho(Temp)=rho_0_cu*(1+gamma*Temp);
L_fil_stator_tb=N_spires_par_phase*(2*Nepp*N_phases*(2*pi*(R_int_stator+hd/2)/N_encoches)+4*L_tetes_bobines);	
h_cond_reduit = sqrt(4*pow(10,-7)*S_fil_stator*w/(rho(T_cu_stator)));
PSI = 2*h_cond_reduit*(sinh(h_cond_reduit)-sin(h_cond_reduit))/(cosh(h_cond_reduit)+cos(h_cond_reduit));
PHI = h_cond_reduit*(sinh(2*h_cond_reduit)+sin(2*h_cond_reduit))/(cosh(2*h_cond_reduit)-cos(2*h_cond_reduit));
Km = PHI+(pow(n_couches,2)-1)/3*PSI;
Rs = rho(T_cu_stator)*(L_fil_stator_tb+N_spires_par_phase*2*lstator*Km)/(fils_en_parallele*S_fil_stator)/pow(3,delta);

/* Parametres divers pour le calcul des pertes fer */
Kc=pas_dentaire/(pas_dentaire-(pow(ouv_encoche,2)/(ouv_encoche+5*entrefer)));
surface_griffes=2*p*ln*(l_base_griffe+l_bout_griffe)/2;

/* Resistance de l'enroulement rotorique */
L_fil_rotor=Nex*2*pi*(Rn+h_plateau/2);
Rr=rho(T_cu_rotor)*L_fil_rotor/S_fil_rotor;

/* Courant d'excitation maximal */
Iex_max=(Ub-Vbb-Vr)/Rr;
Iex=duty_cycle*Iex_max;

/* ---------------------------
Calculs des reluctances 
--------------------------- */

/* Definition de la reluctance d'entrefer */
S_entrefer_2=lstator*(l_base_griffe+l_bout_griffe)/2;
entrefer_moyen=2/(l_base_griffe+l_bout_griffe)*(((l_base_griffe+l_bout_griffe)/2-2*l_chanf)*entrefer+2*l_chanf*(entrefer+h_chanf/2));
R4 = Kc*entrefer_moyen/(mu0*S_entrefer_2);
R6=R4;

/*Definition des longueurs et surfaces utiles pour le calcul des reluctances */
L_noyau=ln+ep;
S_noyau=pi*(pow(Rn,2)-pow(Ra,2))/p;
S_plateau=h_plateau*2*pi*ep/(p*log((Rn+h_plateau)/Rn));
L_coude=sqrt(pow(h_base_griffe,2)+pow(ep,2))/2;
S_coude=l_base_griffe*ep;
L_griffe=sqrt(pow(h_base_griffe,2)+pow(ln,2))/2;
S_griffe=h_base_griffe*l_base_griffe;
S_dents=S_entrefer*largeur_dent/(pas_dentaire-ouv_encoche);
L_culasse=3*(l_fond_encoche+largeur_dent)/2;
S_culasse=h_culasse*lstator;

/* Definition des reluctances variables (non lineaire) */
function R1(flux)=Hr(abs(flux)/S_noyau)*L_noyau/(2*abs(flux))+Hr(abs(flux)/S_plateau)*h_plateau/abs(flux);
function  R2(flux)=Hr(abs(flux)/S_coude)*L_coude/abs(flux);
function  R3(flux)=Hr(abs(flux)/S_griffe)*L_griffe/abs(flux);
function  R5(flux)=2*Hs(abs(flux)/S_dents,f)*hd/abs(flux)+Hs(abs(flux)/(2*S_culasse),f)*L_culasse/abs(flux);
function R9(flux)=R1(flux);
function R8(flux)=R2(flux);
function R7(flux)=R3(flux);


/* Definition des reluctances correspondantes aux flux de fuites */

/* reluctance de fuite entre deux griffes */
/* reluctance utile au calcul de la reluctance de fuites entre griffes par le stator */
alpha_s = l_bout_griffe/(2*R_ext_rotor)-(pas_dentaire-ouv_encoche)/(2*R_int_stator);
beta_s = l_base_griffe/(2*R_ext_rotor)+(pas_dentaire-ouv_encoche)/(2*R_int_stator);
Rgg_stator_entrefer =3*entrefer*(beta_s-alpha_s)*pas_dentaire/(R_int_stator*2*mu0*lstator*(pas_dentaire-ouv_encoche)*(pow(beta_s,2)-pi*beta_s/p+pow(pi/p,2)/4)) ;
Rgg_stator_dent = dgg/(20*mu0*largeur_dent*hd*cos(beta));
alpha_dent = hd/(hd+largeur_dent/2)*2*pi*largeur_dent/sqrt(pow(10,7)*rho_fer_stator*2*pi/(mu_r_dent*w));
coef_effet_peau = alpha_dent*(sinh(2*alpha_dent)+sin(2*alpha_dent))/(cosh(2*alpha_dent)-cos(2*alpha_dent));
Rgg_stator = (Rgg_stator_dent*coef_effet_peau+Rgg_stator_entrefer)/2;
        
/* reluctance de fuite entre deux griffes principale*/
l_gc = ln/sin(beta)-dgg*cos(beta);
hg1 = h_bec+dgg*cos(beta)*tan(xi);
hg2 = h_base_griffe-hg1;
Rgg_principal = hg2/(4*mu0*l_gc*(hg1+hg2/2)*log(dgg/(sqrt(pow(dgg,2)+pow(hg2/2,2))-hg2/2)));
        
/* reluctance de fuite entre deux griffes interieure*/
Rgg_int = pi/(mu0*l_gc*log((dgg+(l_bout_griffe+l_base_griffe)/2)*(sqrt(pow(h_base_bec,2)+pow(dgg,2))+l_bout_griffe)/(dgg*sqrt(pow(h_base_bec,2)+pow(dgg,2)))));
               
/* reluctance de fuite entre griffe*/
Rgg_rotor = Rgg_principal*Rgg_int/(Rgg_principal+Rgg_int);
R18 = Rgg_rotor*Rgg_stator/(Rgg_rotor+Rgg_stator);

/* reluctance de fuite entre un plateau et une griffe */
r_min=0.001;
R10=(xi+pi/2)/(mu0*l_base_griffe*log(h_plateau/r_min));
R11=R10;

/* reluctance de fuite entre un coude et le stator */
R12=3*pi/(4*mu0*3*largeur_dent*log(ep/entrefer));
R13=R12;

/* reluctance de fuite entre griffe et plateau */
R14=pi/(4*mu0*h_bec*log(2*l_bout_griffe/dgg));
R15=R14;

/* reluctance de fuite entre griffe et noyau */
h_moy=(h_base_bec/2)+h_plateau;
e1=(h_moy-dgg)/(2*sin(beta));
e2=l_bout_griffe*tan(beta)/2;
Sgn=(ln-e2)*(l_base_griffe-2*e1)/2;
R16=h_moy/(mu0*Sgn);
R17=R16;

/* Calcul de la pulsation */
w=p*pi*N/30;

/* ----------------------------------------------
Caracteristiques des materiaux magnetiques 
---------------------------------------------- */

/* Pour le stator */
function Hs(B,freq)=70*atan(13*B)*(1+freq/2000)+130*pow(B,2)*(1+atan((freq-1030)/350)*2.25/pi)*6.5+pow(B/1.58,10)*900*(1+atan(15*(B-1.6))*2/pi)+pow(B/2.1,18)*18500*(1-atan(6.8*(B-2.33))*2/pi);

/* Pour le rotor */
function Hr(B)=556.2*pow(B,0.584)+pow(exp(B-2.373),2.949)*4105*pow(B,5.208)/(1+pow(exp(B-2.373),2.949));
     
/* -----------------------------------------------------------------
Definition des parametres intermediaires du modele electrique
----------------------------------------------------------------- */

/* Calcul de la force electromotrice */
fem_d=N_spires_par_phase*abs(psi7)*w/sqrt(2)/pow(sqrt(3),delta);

Er=sqrt(pow(fem_d,2)+pow(Lq*w*Iq,2));

/* Courant efficace de phase */
Is=sqrt((pow(Iactif,2)+pow(Ireactif,2))/2);

/* ------------------------------------------------------------ 
Definition des equations implicites e annuler.
12 equations pour le circuit magnetique, electrique et le couplage 
------------------------------------------------------------ */
c1=(R1(psi1)+R15+R16)*psi1-R15*psi3-R16*psi8-Iex*Nex/2;
c2=(R9(psi2)+R14+R17)*psi2-R14*psi4-R17*psi8-Iex*Nex/2;
c3=-R15*psi1+(R2(psi3+psi9)+R3(psi3+psi5+psi9)+R15+R18)*psi3+R18*psi4+R3(psi3+psi5+psi9)*psi5
-R18*psi7-R18*psi8+(R2(psi3+psi9)+R3(psi3+psi5+psi9))*psi9;
c4=-R14*psi2+(R8(psi4+psi10)+R7(psi4+psi6+psi10)+R14+R18)*psi4+R18*psi3+R7(psi4+psi6+psi10)*psi6
-R18*psi7-R18*psi8+(R8(psi4+psi10)+R7(psi4+psi6+psi10))*psi10;
c5=R3(psi3+psi5+psi9)*psi3+(R3(psi3+psi5+psi9)+R4+R12)*psi5+R4*psi7+R3(psi3+psi5+psi9)*psi9;
c6=R7(psi4+psi6+psi10)*psi4+(R7(psi4+psi6+psi10)+R6+R13)*psi6+R6*psi7+R7(psi4+psi6+psi10)*psi10;
c7=-R18*psi3-R18*psi4+R4*psi5+R6*psi6+(R4+R5(psi7)+R6+R18)*psi7+R18*psi8
   +2*Kri*N_cond_par_encoche*sqrt(2)*Id/pow(sqrt(3),delta);
c8=-R16*psi1-R17*psi2-R18*psi3-R18*psi4+R18*psi7+(R16+R17+R18)*psi8;
c9=(R2(psi3+psi9)+R3(psi3+psi5+psi9))*psi3+R3(psi3+psi5+psi9)*psi5
+(R2(psi3+psi9)+R3(psi3+psi5+psi9)+R10)*psi9;
c10=(R8(psi4+psi10)+R7(psi4+psi6+psi10))*psi4+R7(psi4+psi6+psi10)*psi6
+(R8(psi4+psi10)+R7(psi4+psi6+psi10)+R11)*psi10;
c11=Id-Is*cos(atan(abs(Iactif/Ireactif))-atan(Lq*w*Iq/fem_d));
c12=Iq-Is*sin(atan(abs(Iactif/Ireactif))-atan(Lq*w*Iq/fem_d));

/*-------------------------
Modele du redresseur
------------------------- */
f=w/(2*pi);
T=1/f;
phi=atan(Lf*w/(Rs+Rd));
Z=sqrt(pow((Rs+Rd),2)+pow(Lf*w,2));
tau=Lf/(Rs+Rd);

/* equation du mode binaire */
t000=(pi/3-ExternFunction((Ub+2*Vd)/(sqrt(6)*Er)))/w;
AAA1=((Ub+2*Vd)/(2*(Rs+Rd))-(sqrt(6)*Er)*cos(w*t000-pi/3-phi)/(2*Z))*exp(t000/tau);
ta=3*T/11;
ta2=ta-T/6-phi/w;
aa=AAA1/(2*pow(tau,2)*exp(ta/tau))-(sqrt(6)*Er)*pow(w,2)*cos(w*ta2)/(4*Z);
bb=-AAA1*exp(-ta/tau)*(ta/tau+1)/tau+(sqrt(6)*Er)*w*(w*ta*cos(w*ta2)-sin(w*ta2))/(2*Z);
cc=AAA1*(1+ta/tau+pow(ta,2)/(2*pow(tau,2)))/exp(ta/tau)+(sqrt(6)*Er)*(ta*w*sin(w*ta2)+(1-pow(w*ta,2)/2)*cos(w*ta2))/(2*Z)-(Ub+2*Vd)/(2*(Rs+Rd));
t111=(-bb-sqrt(abs(pow(bb,2)-4*aa*cc)))/(2*aa);
t000bis=t000+T/6;

/* equation du mode mixte */
t1=(ExternFunction(-(Ub+2*Vd)/(sqrt(6)*Er)/sqrt(3))-pi/6)/w;
A2=((sqrt(6)*Er)*cos(w*t1+pi/6-phi)/(Z*sqrt(3))+(Ub+2*Vd)/(3*(Rs+Rd)))*exp(t1/tau)*(1+exp(-T/(6*tau)))/(2-exp(-T/(6*tau)));
A3=A2*(1-2*exp(-T/(6*tau)))/(1+exp(-T/(6*tau)));
A1=(A2-A3)/2;
tt2=T/4+atan(Lf*w/((Rs+Rd)+(Ub+2*Vd)*Z/(sqrt(6)*Er)))*T/(2*pi);
AA=(Rs+Rd)*(sqrt(6)*Er)/(sqrt(3)*Z);
BB=-(Ub+2*Vd)/3;
CC=(Rs+Rd)*A3;
DD=-(phi+pi/6)/w;
tt1=tt2+DD;
a=-CC/(2*exp(tt2/tau)*pow(tau,2))-AA/2*cos(w*tt1)*pow(w,2);
b=AA*(cos(w*tt1)*pow(w,2)*tt2-sin(w*tt1)*w)+CC*(tt2+tau)/(exp(tt2/tau)*pow(tau,2));
c=AA*(cos(w*tt1)*(1-pow(w*tt2,2)/2)+sin(w*tt1)*w*tt2)+BB-CC*(pow(tt2,2)/(2*pow(tau,2))+tt2/tau+1)/exp(tt2/tau);
t0bis=(-b-sqrt(abs(pow(b,2)-4*a*c)))/(2*a);
t0=t0bis-T/6;
Imoyen_mixte=6/T*((Ub+2*Vd)/(6*(Rs+Rd))*(t1-t0-2*T/3)+tau*(A1-A2*exp(-T/(6*tau)))*exp(-t0/tau)+tau*(A2-A1)*exp(-t1/tau)
            +(sqrt(6)*Er)/(2*sqrt(3)*Z*w)*(cos(w*t0-phi-pi/3)+cos(w*t1-phi-pi/3)));
Iactif_mixte=(Ub+2*Vd)/(2*(Rs+Rd)*pi)*(-cos(w*t0)-cos(w*t1)-sqrt(3)*(sin(w*t1)+sin(w*t0)))+2*(sqrt(6)*Er)*sqrt(3)/(T*Z)*(t0+T/6-t1)*cos(phi)
	    +sqrt(3)*(sqrt(6)*Er)/(pi*Z*4)*(2*cos(phi)*w*(t1-t0)-sin(2*w*t1+pi/3-phi)+sin(2*w*t0+pi/3-phi))
	    +2*tau*sqrt(3)/(T*(1+pow(w*tau,2)))*((w*tau*(A2-A3)-sqrt(3)*(A2+A3))*exp(-t0bis/tau)*sin(w*t0)
	    -(sqrt(3)*w*tau*(A3+A2)+(A2-A3))*exp(-t0bis/tau)*cos(w*t0)+(sqrt(3)*(A2-A1)+w*tau*(A2+2*A3+A1))*exp(-t1/tau)*sin(w*t1)
	    -(sqrt(3)*w*tau*(A1-A2)+(A2+2*A3+A1))*exp(-t1/tau)*cos(w*t1)+(sqrt(3)-w*tau)*A1*exp(-t0/tau)*sin(w*t0)+(w*tau*sqrt(3)+1)*A1*exp(-t0/tau)*cos(w*t0));
Ireactif_mixte=(Ub+2*Vd)/(2*(Rs+Rd)*pi)*(sin(w*t0)+sin(w*t1)-sqrt(3)*(cos(w*t0)+cos(w*t1)))-2*(sqrt(6)*Er)*sqrt(3)/(T*Z)*(t0+T/6-t1)*sin(phi)
	    +sqrt(3)*(sqrt(6)*Er)/(pi*Z*4)*(2*sin(phi)*w*(t0-t1)+cos(2*w*t0+pi/3-phi)-cos(2*w*t1+pi/3-phi))
	    +2*tau*sqrt(3)/(T*(1+pow(w*tau,2)))*((sqrt(3)*w*tau*(A2+A3)+(A2-A3))*exp(-t0bis/tau)*sin(w*t0)
	    +(w*tau*(A2-A3)-sqrt(3)*(A2+A3))*exp(-t0bis/tau)*cos(w*t0)+(sqrt(3)*(A2-A1)+w*tau*(A2+2*A3+A1))*exp(-t1/tau)*cos(w*t1)
	    +(sqrt(3)*w*tau*(A1-A2)+(A2+2*A3+A1))*exp(-t1/tau)*sin(w*t1)+(sqrt(3)-w*tau)*A1*exp(-t0/tau)*cos(w*t0)-(w*tau*sqrt(3)+1)*A1*exp(-t0/tau)*sin(w*t0));

/* equation du mode triphasee */
AAA=(Ub+2*Vd)/(3*(Rs+Rd))*(exp(T/(6*tau))-exp(-T/(6*tau)))*sqrt(3)*Z/(sqrt(6)*Er);
BBB=exp(T/(6*tau))+exp(-T/(6*tau))-2;
t00i=T/6+atan(Lf*w/((Rs+Rd)+(Ub+2*Vd)*Z/(sqrt(6)*Er)))*T/(2*pi);
ttt1=t00i+(pi/6-phi)/w;
ttt2=t00i+(2*pi/3-phi)/w;
aaa=-(BBB*cos(w*ttt1)+sin(w*ttt2))*pow(w,2)/2;
bbb=((cos(w*ttt1)*w*t00i-sin(w*ttt1))*BBB+cos(w*ttt2)+sin(w*ttt2)*w*t00i)*w;
ccc=(cos(w*ttt1)*(1-pow(w*t00i,2)/2)+w*sin(w*ttt1)*t00i)*BBB-w*cos(w*ttt2)*t00i-AAA+sin(w*ttt2)*(1-pow(w*t00i,2)/2);
t00=(-bbb-sqrt(abs(pow(bbb,2)-4*aaa*ccc)))/(2*aaa);
t00bis=t00+T/6;
AA3=((sqrt(6)*Er)/(sqrt(3)*Z)*cos(w*t00+pi/6-phi)-(Ub+2*Vd)/(3*(Rs+Rd)))*exp(t00bis/tau);
AA2=(sqrt(6)*Er)/(sqrt(3)*Z)*sin(w*t00+2*pi/3-phi)*exp(t00/tau)/(1-exp(-T/(6*tau)));
Imoyen_tri=6/T*(AA2*tau*exp(-t00/tau)*(1-exp(-T/(6*tau)))+(sqrt(6)*Er)/(sqrt(3)*Z*w)*cos(w*t00-phi-pi/3)-T*(Ub+2*Vd)/(9*(Rs+Rd)));
Ireactif_tri=-4*(Ub+2*Vd)/(w*T*(Rs+Rd))*(sin(w*t00+pi/3)-sin(w*t00))-(sqrt(6)*Er)/(sqrt(3)*Z)*sin(phi)
	    +2*sqrt(3)*tau/(T*(1+pow(w*tau,2)))*((AA2+2*AA3-sqrt(3)*AA2*w*tau)*(exp(-t00/tau)*sin(t00*w)-exp(-t00bis/tau)*sin(t00bis*w))
	    +(AA2*w*tau+2*AA3*w*tau+sqrt(3)*AA2)*(exp(-t00/tau)*cos(t00*w)-exp(-t00bis/tau)*cos(t00bis*w)));
Iactif_tri=2*(sqrt(6)*Er)*sqrt(3)*cos(phi)/(Z*T*3*w)*pi+4*(Ub+2*Vd)/(w*T*(Rs+Rd))*(cos(w*t00+pi/3)-cos(w*t00))
	    +2*tau/(T*(1+pow(w*tau,2)))*((2*sqrt(3)*AA3*w*tau+sqrt(3)*AA2*w*tau+3*AA2)*(exp(-t00/tau)*sin(t00*w)-exp(-t00bis/tau)*sin(t00bis*w))
	    +(-2*sqrt(3)*AA3-sqrt(3)*AA2+3*AA2*w*tau)*(exp(-t00/tau)*cos(t00*w)-exp(-t00bis/tau)*cos(t00bis*w)));


/*  Determination des coefficients de ponderation */
k1=(0.5+atan(10000*f*(t0-t1))/pi)*(0.5-atan(10000*(Ub+2*Vd-(sqrt(6)*Er))/(sqrt(6)*Er))/pi);
k2=(0.5+atan(10000*f*(t1-t0))/pi)*(0.5+atan(10000*f*(t111-t000bis))/pi)*(0.5-atan(10000*(Ub+2*Vd-(sqrt(6)*Er))/(sqrt(6)*Er))/pi);

/* Calcul des grandeurs de sortie du modele du redresseur */
Imoyen=k1*Imoyen_tri+k2*Imoyen_mixte;
Iactif=k1*Iactif_tri+k2*Iactif_mixte;
Ireactif=k1*Ireactif_tri+k2*Ireactif_mixte;


/* -------------------------------------
Calculs utiles au dimensionnement
------------------------------------- */

/* Calcul de la puissance fournie */
P_electrique=Imoyen*Ub;

/* Calcul des inductions */
B_noyau=abs(psi1)/S_noyau;
B_plateau=abs(psi1)/S_plateau;
B_coude=abs(psi3+psi9)/S_coude;
B_griffe=abs(psi3+psi5+psi9)/S_griffe;
B_entrefer=abs(psi5+psi7)/S_entrefer;
B_dents=abs(psi7)/S_dents;
B_culasse=abs(psi7)/(2*S_culasse);

/* Calcul du coefficient de foisonnement de la bobine d'excitation */
foisonnement_bob_rotor=S_fil_rotor*Nex/(ln*h_plateau);

/* Calcul du coefficient de remplissage d'encoche */
l_encoche_pied=2*pi*(R_int_stator+h_pied)/N_encoches-largeur_dent;
l_encoche_semelle=2*pi*(R_int_stator+h_semelle)/N_encoches-(pas_dentaire-ouv_encoche);
S_encoche=(l_encoche_pied+l_fond_encoche)*(hd-h_pied)/2+(l_encoche_pied+l_encoche_semelle)*(h_pied-h_semelle)/2;
remplissage_encoche=N_cond_par_encoche*fils_en_parallele*S_fil_stator/S_encoche;

/* Calcul des densites de courant */
delta_rotor=Iex/S_fil_rotor;
delta_stator=Is/(fils_en_parallele*S_fil_stator);


/* ----------------------
Calculs des masses
---------------------- */

/* masses de cuivre */
M_cu_rotor=M_v_cu*L_fil_rotor*S_fil_rotor;
M_cu_stator=M_v_cu*N_phases*fils_en_parallele*(L_fil_stator_tb+N_spires_par_phase*2*lstator)*S_fil_stator;

/* volumes des zones de fer */
V_noyau=pi*(pow(Rn,2)-pow(Ra,2))*(ln+2*ep);
V_plateau=pi*(pow(Rn+h_plateau,2)-pow(Rn,2))*ep;
V_coude=3*ep*l_base_griffe*h_base_griffe/4;
V_griffe=(l_base_griffe+l_bout_griffe)*ln*(h_bec+h_base_bec/2)/2;
V_dent=lstator*(largeur_dent*(hd-h_pied)+(h_pied-h_semelle)*(pas_dentaire-ouv_encoche+largeur_dent)/2+h_semelle*(pas_dentaire-ouv_encoche));
V_culasse=pi*(pow(R_ext_stator,2)-pow(R_ext_stator-h_culasse,2))*lstator;

/* masses de fer */
M_fer_rotor=M_v_fer*(V_noyau+2*V_plateau+2*p*(V_coude+V_griffe));
M_fer_dents=M_v_fer*N_encoches*V_dent;
M_fer_culasse=M_v_fer*V_culasse;
M_fer_stator=M_fer_dents+M_fer_culasse;

/* masse totale de l'alternateur */
masse=M_fer_stator+M_fer_rotor+M_cu_stator+M_cu_rotor+M_sup;

/* -----------------------------------
Modeles des pertes et rendement
----------------------------------- */

/* Pertes joules au stator */
P_j_s=3*Rs*pow(Is,2);

/* Pertes dans le redresseur */
P_red=6*Is*(sqrt(2)*Vd/pi+Rd*Is/2);

/* Pertes de l'excitation */
P_ex=Ub*Iex;

/* Pertes fer dans le stator */
P_fer_dents=(k_hyst*w/(2*pi)*pow(B_dents,steinmetz)+4*3*Nepp/pow(pi,2)*k_eddy*pow(w/(2*pi),2)*pow(B_dents,2))*M_fer_dents;
P_fer_culasse=(k_hyst*w/(2*pi)*pow(B_culasse,steinmetz)+k_eddy*pow(w/(2*pi),2)*pow(B_culasse,2))*M_fer_culasse;
P_fer_stator=P_fer_dents+P_fer_culasse;

/* Pertes fer dans le rotor */
mu_r_surface_griffe=B_entrefer/(mu0*Hr(B_entrefer));
Ks=sqrt(pow(10,7)/(mu_r_surface_griffe*rho_fer_griffe))/(32*pi);
P_fer_enc_rotor=correction_pertes*surface_griffes*Ks*pow(Kc-1,2)*pow(B_entrefer,2)*pow(pi*N*R_ext_rotor/30,1.5)*pow(ouv_encoche,-0.5)*pas_dentaire;
P_fer_harm_rotor=correction_pertes*surface_griffes*Ks*74/1225*pow(3*mu0*N_cond_par_encoche*Is*sqrt(2)/(pi*entrefer),2)*pow(pi*N*R_ext_rotor/30,1.5)*pow(pas_dentaire,0.5);

/* Pertes mecaniques et aerauliques */
P_meca=K_meca*N/2000;
P_aero=K_aero*pow(N/2000,3);

P_absorbee=P_electrique+P_j_s+P_red+P_ex+P_fer_stator+P_fer_enc_rotor+P_fer_harm_rotor+P_meca+P_aero;
rendement=100*P_electrique/P_absorbee;

Le modèle ExternFunction

       

package website.java;

import org.gu.vesta.muse.v5.JacobianFacet;
import org.gu.vesta.muse.v5.JacobianFacet.ComputeJacobian;
import org.gu.vesta.muse.v5.MuseModel;
import org.gu.vesta.muse.v5.StaticFacet;
import org.gu.vesta.muse.v5.StaticFacet.Compute;

/*
 * ExternFunction.java
 * Copyright (c) G2Elab & Vesta-System.
 * Use, duplication or distribution is subject to authorization.
 * For more informations see:
 * www.cades-solutions.com
 * www.vesta-system.com
 */
@MuseModel(name="m1")
public class ExternFunction {
    
    /** Creates a new instance of ExternFunction */
    public ExternFunction() {
    }
    

    @StaticFacet(museModel="m1")
    @Compute
    public double realAcos(double x) {
        if(x<-1.0)
        {
            return Math.PI;
        }
        if(x>1.0)
        {
            return 0;
        }
        else
        {
            return Math.acos(x);
        }
    }
    
    @JacobianFacet(museModel="m1")
    @ComputeJacobian
    public double[] jacobian_realAcos(double x) {
        double result;
	if(x<-1.0)
        {
            result = 0;
        }
        if(x>1.0)
        {
            result = 0;
        }
        else
        {
            result = -1/Math.sqrt(1-Math.pow(x,2));
        }
        return new double[] {result};
    }
}

L’optimisation

Le scénario d’optimisation est le suivant :

• Trouver la valeur optimale de :
• ep
• h_bec
• h_plateau
• hd
• Id
• Iq
• l_base_griffe
• l_bout_griffe
• largeur_dent
• ln
• lstator
• N_cond_par_encoche
• Nex
• ouv_encoche
• psi1
• psi10
• psi2
• psi3
• psi4
• psi5
• psi6
• psi7
• psi8
• psi9
• R_ext_rotor
• R_ext_stator
• R_int_stator
• Rn
• S_fil_rotor
• S_fil_stator
• Tel que :
• Le rendement soit supérieur à 70% (rendement)
• La puissance électrique soit supérieure à 750W (P_electrique)
• Les inductions dans les pièces ferromagnétiques soient inférieures à 2T pour éviter la saturation (B_coude, B_culasse, B_dents, B_entrefer, B_griffe, B_noyau, B_plateau)
• Les lois de Kirchhoff dans le circuit magnétique et électrique soient respectés (c1 .. c12 = 0 ± 1e-7)
• La masse de l’alternateur soit minimale (masse)
• Pour une valeur imposée de toutes les autres variables d’entrée

Le cahier des charges

    

/*Les intervalles de libertés d’optimisation*/
ep                  - Interval = [0.005..0.013]   - valeur initiale = 0.0122
h_bec               - Interval = [0.001..0.03]    - valeur initiale = 0.0025
h_plateau           - Interval = [0.001..0.03]    - valeur initiale = 0.0117
hd                  - Interval = [0.005..0.02]    - valeur initiale = 0.0105
Id                  - Interval = [0.0..200.0]     - valeur initiale = 26.91
Iq                  - Interval = [0.0..150.0]     - valeur initiale = 32.32
l_base_griffe	    - Interval = [0.02..0.06]     - valeur initiale = 0.0283
l_bout_griffe	    - Interval = [0.003..0.02]    - valeur initiale = 0.0065
largeur_dent	    - Interval = [0.002..0.01]    - valeur initiale = 0.0034
ln                  - Interval = [0.01..0.034]    - valeur initiale = 0.03245
lstator	            - Interval = [0.01..0.034]    - valeur initiale = 0.03305
N_cond_par_encoche  - Interval = [5.0..10.0]      - valeur initiale = 8.0
Nex                 - Interval = [300.0..600.0]   - valeur initiale = 370.0
ouv_encoche         - Interval = [0.0028..0.004]  - valeur initiale = 0.0028
psi1	            - Interval = [-0.001..0.001]  - valeur initiale = 5.470850189E-4
psi10	            - Interval = [-0.001..0.001]  - valeur initiale = -7.340152E-6
psi2	            - Interval = [-0.001..0.001]  - valeur initiale = 5.470850189E-4
psi3	            - Interval = [-0.001..0.001]  - valeur initiale = 5.454755E-4
psi4	            - Interval = [-0.001..0.001]  - valeur initiale = 5.454755E-4
psi5	            - Interval = [-0.001..0.001]  - valeur initiale = -7.75419E-6
psi6	            - Interval = [-0.001..0.001]  - valeur initiale = -7.75419E-6
psi7	            - Interval = [1.0E-6..0.001]  - valeur initiale = 4.2949665E-4
psi8	            - Interval = [-0.001..0.001]  - valeur initiale = 5.5845326E-4
psi9	            - Interval = [-0.001..0.001]  - valeur initiale = -7.340152E-6
R_ext_rotor         - Interval = [0.04..0.06]     - valeur initiale = 0.05265
R_ext_stator	    - Interval = [0.06..0.068]    - valeur initiale = 0.06775
R_int_stator	    - Interval = [0.04..0.06]     - valeur initiale = 0.053
Rn                  - Interval = [0.02..0.04]     - valeur initiale = 0.02965
S_fil_rotor         - Interval = [2.0E-7..1.5E-6] - valeur initiale = 7.4E-7
S_fil_stator	    - Interval = [1.0E-6..3.0E-6] - valeur initiale = 1.54E-6

/*Les variables imposées*/
duty_cycle        - Fixe - valeur = 1.0
fils_en_parallele - Fixe - valeur = 2.0
gamma             - Fixe - valeur = 0.004
h_chanf           - Fixe - valeur = 5.0E-4
h_pied            - Fixe - valeur = 0.0015
h_semelle         - Fixe - valeur = 0.001
K_aero            - Fixe - valeur = 1.73
k_eddy            - Fixe - valeur = 3.7E-4
k_hyst            - Fixe - valeur = 0.044
K_meca            - Fixe - valeur = 17.919
l_chanf           - Fixe - valeur = 0.0015
L_tetes_bobines   - Fixe - valeur = 0.008
M_sup             - Fixe - valeur = 0.0
M_v_cu            - Fixe - valeur = 8960.0
M_v_fer           - Fixe - valeur = 7870.0
mu_r_dent         - Fixe - valeur = 1000.0
N                 - Fixe - valeur = 1500.0
n_couches         - Fixe - valeur = 5.0
N_phases          - Fixe - valeur = 3.0
Nepp              - Fixe - valeur = 1.0
p                 - Fixe - valeur = 6.0
Ra                - Fixe - valeur = 0.00865
Rd                - Fixe - valeur = 0.0094
rho_0_cu          - Fixe - valeur = 1.72E-8
rho_fer_griffe    - Fixe - valeur = 9.7E-8
rho_fer_stator    - Fixe - valeur = 2.2E-7
steinmetz         - Fixe - valeur = 1.62
T_cu_rotor        - Fixe - valeur = 130.0
T_cu_stator       - Fixe - valeur = 120.0
Ub                - Fixe - valeur = 14.0
Vbb               - Fixe - valeur = 0.75
Vd                - Fixe - valeur = 0.75
Vr                - Fixe - valeur = 0.8

/*Les contraintes sur les sortie*/
B_coude	               - Interval = [0.01..2.0]
B_culasse              - Interval = [0.01..2.0]
B_dents                - Interval = [0.01..2.0]
B_entrefer             - Interval = [0.01..2.0]
B_griffe               - Interval = [0.01..2.0]
B_noyau                - Interval = [0.01..2.0]
B_plateau              - Interval = [0.01..2.0]
c1                     - Interval = [-1.0E-7..1.0E-7]
c10                    - Interval = [-1.0E-7..1.0E-7]
c11                    - Interval = [-1.0E-7..1.0E-7]
c12                    - Interval = [-1.0E-7..1.0E-7]
c2                     - Interval = [-1.0E-7..1.0E-7]
c3                     - Interval = [-1.0E-7..1.0E-7]
c4                     - Interval = [-1.0E-7..1.0E-7]
c5                     - Interval = [-1.0E-7..1.0E-7]
c6                     - Interval = [-1.0E-7..1.0E-7]
c7                     - Interval = [-1.0E-7..1.0E-7]
c8                     - Interval = [-1.0E-7..1.0E-7]
c9                     - Interval = [-1.0E-7..1.0E-7]
contrainte_trapeze     - Interval = [0.001..0.1]
delta_rotor            - Interval = [1.0..2.0E7]
delta_stator           - Interval = [1.0..5.0E7]
dgg                    - Interval = [0.002..0.03]
ecart_longueur         - Interval = [0.0..0.001]
entrefer               - Interval = [2.5E-4..0.003]
foisonnement_bob_rotor - Interval = [0.0..0.7]
h_base_bec             - Interval = [0.001..0.03]
h_culasse              - Interval = [0.001..0.04]
Imoyen                 - Interval = [54.4..54.5]
l_fond_encoche         - Interval = [0.001..0.03]
P_electrique           - Interval = [750.0..1500.0]
rdm_griffe             - Interval = [0.0..2.9]
remplissage_encoche    - Interval = [0.0..0.4]
rendement              - Interval = [70.0..100.0]
masse                  - Minimize                   - valuer = 5.0 - weight = 1.0		

/*L'optimiseur*/
Optimizer = SQP
Optimizer.Precision     = 1.0E-5
Optimizer.Max Iteration = 100

Le résultat d’optimisation

    

/*Les valeurs d'entrée trouvées*/
Nex                 - valeur initiale = 370.0          - valeur trouvée = 358.7339994276839
N_cond_par_encoche  - valeur initiale = 8.0            - valeur trouvée = 9.862251072216864
R_ext_stator        - valeur initiale = 0.06775        - valeur trouvée = 0.06699860773574176
R_int_stator        - valeur initiale = 0.053          - valeur trouvée = 0.0466097249149832
R_ext_rotor         - valeur initiale = 0.05265        - valeur trouvée = 0.0463597249149832
Rn                  - valeur initiale = 0.02965        - valeur trouvée = 0.026628123788948545
l_base_griffe       - valeur initiale = 0.0283         - valeur trouvée = 0.03671378850385128
lstator             - valeur initiale = 0.03305        - valeur trouvée = 0.02181424795527241
ln                  - valeur initiale = 0.03245        - valeur trouvée = 0.020814247955272414
hd                  - valeur initiale = 0.0105         - valeur trouvée = 0.015419040172520306
ep                  - valeur initiale = 0.0122         - valeur trouvée = 0.00927198674686363
l_bout_griffe       - valeur initiale = 0.0065         - valeur trouvée = 0.003 (limite min)
ouv_encoche         - valeur initiale = 0.0028         - valeur trouvée = 0.0028 (limite min)
largeur_dent        - valeur initiale = 0.0034         - valeur trouvée = 0.003672697111407895
h_plateau           - valeur initiale = 0.0117         - valeur trouvée = 0.010854414083606923
h_bec               - valeur initiale = 0.0025         - valeur trouvée = 0.001  (limite min)
S_fil_stator        - valeur initiale = 1.54E-6        - valeur trouvée = 1.7153412826908718E-6  (limite max)
psi7                - valeur initiale = 4.2949665E-4   - valeur trouvée = 3.312057012570586E-4
S_fil_rotor         - valeur initiale = 7.4E-7         - valeur trouvée = 4.408518554986462E-7 (limite max)
Iq                  - valeur initiale = 32.32          - valeur trouvée = 27.64281022274342
Id                  - valeur initiale = 26.91          - valeur trouvée = 31.47828341950079
psi9                - valeur initiale = -7.340152E-6   - valeur trouvée = -2.369073390956402E-6
psi8                - valeur initiale = 5.5845326E-4   - valeur trouvée = 4.902561822028892E-4
psi6                - valeur initiale = -7.75419E-6    - valeur trouvée = -5.404802613228786E-6
psi5                - valeur initiale = -7.75419E-6    - valeur trouvée = -5.404802613228786E-6
psi4                - valeur initiale = 5.454755E-4    - valeur trouvée = 4.824918051340233E-4
psi3                - valeur initiale = 5.454755E-4    - valeur trouvée = 4.824918051340231E-4
psi2                - valeur initiale = 5.470850189E-4 - valeur trouvée = 4.832341841103402E-4
psi10               - valeur initiale = -7.340152E-6   - valeur trouvée = -2.369073390956402E-6
psi1                - valeur initiale = 5.470850189E-4 - valeur trouvée = 4.8323418411033974E-4

/*Les valeurs de sorties trouvées*/
masse                  - valeur = 3.06021037386753 (Minimisée) 
P_electrique           - valeur = 761.599610352304
rendement              - valeur = 69.99999200421388 (limite min)
Imoyen                 - valeur = style="color:DodgerBlue">54.39997216802171 (limite min)
delta_stator           - valeur = 1.221121023154052E7
delta_rotor            - valeur = 6590898.831750753
B_plateau              - valeur = 1.567682541018877
B_noyau                - valeur = 1.4551547464436858
B_griffe               - valeur = 1.4565689981467054
B_entrefer             - valeur = 1.0476842658386833
B_dents                - valeur = 1.5471046542881568
B_culasse              - valeur = 1.5275130329138682
B_coude                - valeur = 1.4104258677240165
dgg                    - valeur = 0.0034325053493829212
l_fond_encoche         - valeur = 0.007153364705822553
h_culasse              - valeur = 0.004969842648238257
h_base_bec             - valeur = 0.007877187042427729
contrainte_trapeze     - valeur = 0.033713788503851275
entrefer               - valeur = 2.500000000000002E-4 (limite min)
remplissage_encoche    - valeur = 0.39999998148404264
rdm_griffe             - valeur = 2.3446895796824556
foisonnement_bob_rotor - valeur = 0.7000001016984344 (limite max)
ecart_longueur         - valeur = 9.999999999999974E-4 (limite max)
c9                     - valeur = 0.0024100208129809175 (limite max)
c8                     - valeur = -0.0016992662494885735 (limite min)
c7                     - valeur = 0.0011423838803352737 (limite max)
c6                     - valeur = 0.00235477534367895 (limite max)
c5                     - valeur = 0.0023547753435940177 (limite max)
c4                     - valeur = 0.003944981722091984 (limite max)
c3                     - valeur = 0.003944981955832594 (limite max)
c2                     - valeur = -6.406115659274292E-4  (limite min)
c12                    - valeur = 7.016416752492205E-6 (limite max)
c11                    - valeur = 2.181903182574274E-5 (limite max)
c10                    - valeur = 0.0024100208130946044 (limite max)
c1                     - valeur = -6.406117987580728E-4  (limite min)

Le post-processing

Le post-processeur de Cades peut servir pour montrer l’évolution de la fonction objectif à travers d’itérations d’optimisation :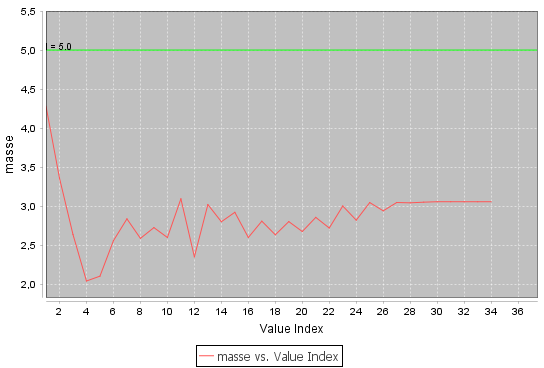

Electroaimant

Cet exemple montre :

1. le circuit et les équations permettant de calculer la force dans l’entrefer
2. l’optimisation mono-objectif (minimisation de la masse du dispositif)

Modélisation

L’objectif de la modélisation est de mettre en place le circuit magnétique (à base des réluctances) et de calculer analytiquement la force et la masse du dispositif.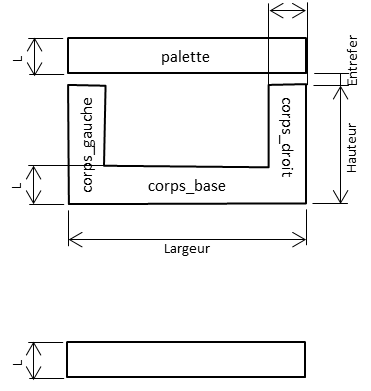

Les paramètres d’entrée

Entrefer	Entrefer du dispositif [mm]
Hauteur	La hauteur du dispositif [mm]
I	Le courant d’alimentation de la bobine [-]
L	L’épaisseur du dispositif [mm]
Largeur	La largeur du dispositif [mm]
N	Le nombre de tours dans les bobines [-]

Le circuit

    

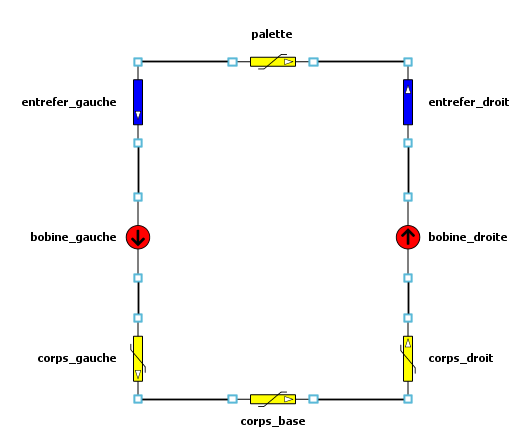
Les paramètres des composants du circuit

• entrefer_droit, entrefer_gauche:
• type: AIRREL
• L = Entrefer
• S = L*L
• corps_droit, corps_gauche:
• type: SATREL
• L = Hauteur – L
• S = L*L
• a = 0.25
• alpha = 1.5
• beta = 1.5
• freq = 50.0
• Js = 1.7
• Kc = 4.98e-5
• Ke = 6.31e-4
• Kh = 0.0187
• mur = 800.0
• vol_mass = 7800.0
• corps_base, palette:
• type: SATREL
• L = Largeur
• S = L*L
• a = 0.25
• alpha = 1.5
• beta = 1.5
• freq = 50.0
• Js = 1.7
• Kc = 4.98e-5
• Ke = 6.31e-4
• Kh = 0.0187
• mur = 800.0
• vol_mass = 7800.0
• bobine_droite, bobine_gauche:
• type: SRC
• I = I
• N = N

Les équations

    

/*Masse du nouyau*/
m = (2*L*Largeur + 2*(Hauteur - L)*L)*L*7800*1.0e-9;

/*Hauteur totale*/
h = Hauteur + Entrefer + L;

/*Force eletromagnetique dans l'entrefer*/
f = pow(entrefer_droit.B,2) * L * L * 1.0e-6/mu0;

L’optimisation

Le scénario d’optimisation est le suivant :

• Trouver la valeur optimale de :
• L’épaisseur du dispositif (L)
• Courant (I)
• Tel que :
• La force dans l’entrefer soit supérieure à 800N (f)
• L’induction dans l’entrefer soit inférieure à 2.0T pour éviter la saturation (entrefer_droit.B)
• La masse du noyau soit minimale (m)
• Pour une valeur imposée de:
• Nombre de tours de 219 (N)
• Entrefer de 2.0mm (Entrefer)
• Largeur de 65.0mm (Largeur)
• Hauteur de 50.0mm (Hauteur)

Le cahier des charges

    

/*Les intervalles de libertés d’optimisation*/
I  - Interval = [0.0..20.0]     - valeur initiale = 20.0
L  - Interval = [8.0..20.0]      - valeur initiale = 15.0

/*Les variables d'entrée imposées*/
Entrefer - Fixe - valeur = 2.0
Hauteur  - Fixe - valeur = 50.0
Largeur  - Fixe - valeur = 65.0 
N        - Fixe - valeur = 219

/*Les contraintes sur les sortie*/
m                - Minimize - valuer = 0.5    - weight = 1.0
f                - Interval = [800.0..2000.0]
entrefer_droit.B - Interval = [0.0..1.6]

/*L'optimiseur*/
Optimizer = SQP
Optimizer.Precision     = 1.0E-5
Optimizer.Max Iteration = 100

Le résultat d’optimisation

    

/*Les valeurs d'entrée trouvées*/
I  - valeur initiale = 20.0 - valeur trouvée = 14.82
L  - valeur initiale = 15.0 - valeur trouvée = 19.81

/*Les valeurs de sorties trouvées*/
m                - valeur = 0.58 (Minimisée) 
f                - valeur = 799.99 (limite min)
entrefer_droit.B - valeur = 1.599 (limite max)

Machine synchrone

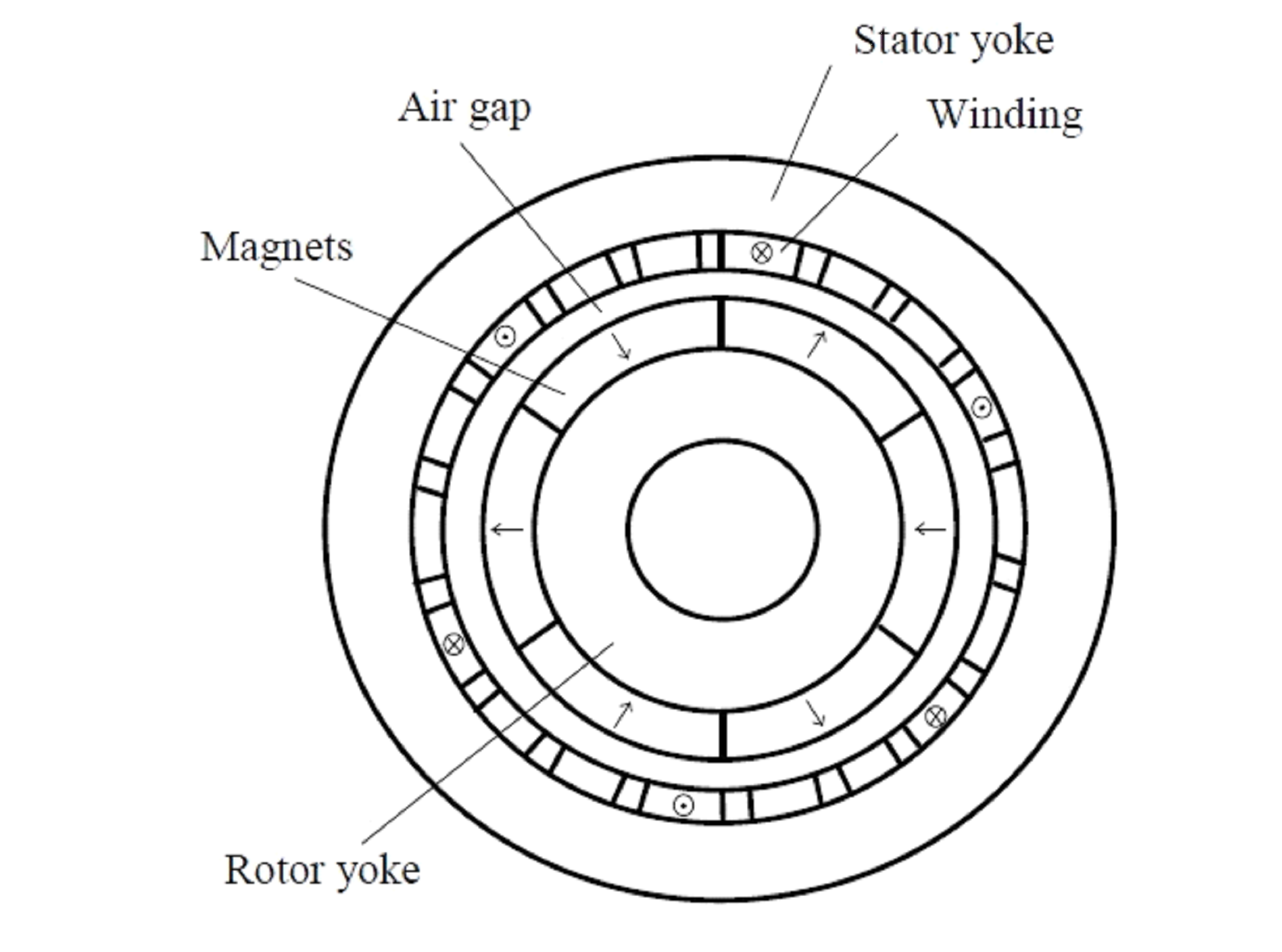
Cet exemple montre :

1. les équations permettant de calculer les pertes joules dans la machine
2. l’optimisation mono-objectif (minimisation des pertes joules)

Modélisation

Les paramètres d’entrée du modèle sont les suivants:

ag	Entrefer [m]
beta	Rapport entre l’angle polaire d’un aimant et le l’angle polaire total [-]
bfer	L’induction dans le noyau [T]
d	Diamètre d’alésage [m]
deltap	Le double du pas polaire [m]
ff	Coefficient de remplissage de l’enroulement [-]
jcu	Densité de courant dans l’enroulement [A/m2]
l	Longueur active de la machine [m]
m	Magnétisation [A/m]
ml	L’épaisseur de l’aimant [m]
wjl	Poids des pertes joules (pour le calcul de la fonction objectif pondérée)[-]
wmv	Poids du volume de l’aimant (pour le calcul de la fonction objectif pondérée) [-]
wjl	Poids du volume net (pour le calcul de la fonction objectif pondérée) [-]
wt	Épaisseur du bobinage [m]

Les équations

       

/*
Machine synchrone

machine_synchrone.sml

Références:
Le dimensionnement des actionneurs é1ectriques : un problème
de programmation non linéaire - J. Phys. III France 3 (1993) p. 285-301.
*/

/*Machine form factor*/
lambda = d/l;

/*Pole count*/
p = pi*d/deltap;

/*Core loss coefficient */
kl = 1.5*p*beta*(ag + wt)/d;

/*Linear current density*/
a = ff*wt*jcu;

/*Joule heating parameter*/
jh = a*jcu;

/*No load ag induction*/
be = (2*ml*m)/(d*log((d + 2*wt)/(d - 2*(ml + ag))));

/*Electromagnetic torque*/
Tem = pi/(2*lambda)*(1 - kl)*sqrt(ff*beta*jh*wt)*pow(d,2)*(d + wt)*be;

/*Yoke thickness*/
y = d*pi*beta*be/(4*p*bfer);

/*Net volume*/
net_volume = pi*d/lambda*(d + wt - ag - ml)*(2*y + wt + ag + ml);

/*Magnet volume*/
magnet_volume = pi*beta*ml*d/lambda*(d - 2*ag - ml); 

/*Joule loss*/
jl = pi*rhocu*d/lambda*(d + wt)*jh; 

/*Multi objective*/
mobj=wjl*jl+wnv*net_volume+wmv*magnet_volume; 

/* Physical constants */
intern muzero;
muzero = 4*pi*1e-7; //Vacuum permeability
rhocu = 1.7908e-8; //Conductor resistivity

L’optimisation

Le scénario d’optimisation est le suivant :

• Trouver la valeur optimale de :
• L’entrefer de la machine(ag)
• L’angle polaire (beta)
• Diamètre de l’alésage (m)
• Densité de courant (jcu)
• Longueur active de la machine (l)
• L’épaisseur de l’aimant (ml)
• L’épaisseur de l’enroulement (wt)
• Tel que :
• Les pertes Joules soient minimales (jl)
• L’induction à vide dans l’entrefer soit au maximum 1.0T (be)
• Le coefficient des pertes fer soit au maximum 0.5 (kl)
• L’épaisseur de la culasse soit au maximum 0.05 (y)
• Le couple électromagnétique soit au maximum 10.0N.m (Tem)
• Le nombre de pôles soit imposé à 4 (p)
• Le paramètre des pertes joules soit 1e11 (jh)
• Pour une valeur imposée de toutes les autres variables d’entrée

Le cahier des charges

    

/*Les intervalles de libertés d’optimisation*/
ag   - Interval = [0.001..0.005] - valeur initiale = 0.00255
beta - Interval = [0.8..1.0]     - valeur initiale = 0.9
d    - Interval = [0.01..0.5]    - valeur initiale = 0.255
jcu  - Interval = [1.0e5..1.0e7] - valeur initiale = 5050000
l    - Interval = [0.004..0.5]   - valeur initiale = 0.252
ml   - Interval = [0.001..0.05]  - valeur initiale = 0.0255
wt   - Interval = [0.001..0.05]  - valeur initiale = 0.012525

/*Les variables d'entrée imposées*/
bfer   - Fixe - valeur = 1.5
deltap - Fixe - valeur = 0.1
ff     - Fixe - valeur = 0.7
m      - Fixe - valeur = 0.9
wjl    - Fixe - valeur = 0.0 
wmv    - Fixe - valeur = 0.0
wnv    - Fixe - valeur = 0.0

/*Les variables de sortie imposées*/
jh  - Fixe - valeur = 1e11
p   - Fixe - valeur = 4.0
Tem - Fixe - valeur = 10.0

/*Les contraintes sur les sortie*/
jl - Minimize                 - valeur = 3822.5 - weight = 1.0
be - Interval = [0.1..1.0]
kl - Interval = [0.01..0.5]
y  - Interval = [0.001..0.05]

/*L'optimiseur*/
Optimizer = SQP
Optimizer.Precision     = 1.0E-5
Optimizer.Max Iteration = 100

Le résultat d’optimisation

    

/*Les valeurs d'entrée trouvées*/
ag    - valeur initiale = 0.00255  - valeur trouvée = 0.001 (limite min)
beta  - valeur initiale = 0.9      - valeur trouvée = 1.0 (limite max)
jcu   - valeur initiale = 5050000  - valeur trouvée = 5228365.95 (Minimisée) 
jcu   - valeur initiale = 5050000  - valeur trouvée = 5228365.95
l     - valeur initiale = 0.252    - valeur trouvée = 0.047
ml    - valeur initiale = 0.0255   - valeur trouvée = 0.021
wt    - valeur initiale = 0.012525 - valeur trouvée = 0.0052

/*Les valeurs de sorties trouvées*/
jl - valeur = 35.26 (Minimisée) 
be - valeur = 0.59
kl - valeur = 0.29
y  - valeur = 0.0098

Convertisseur flyback

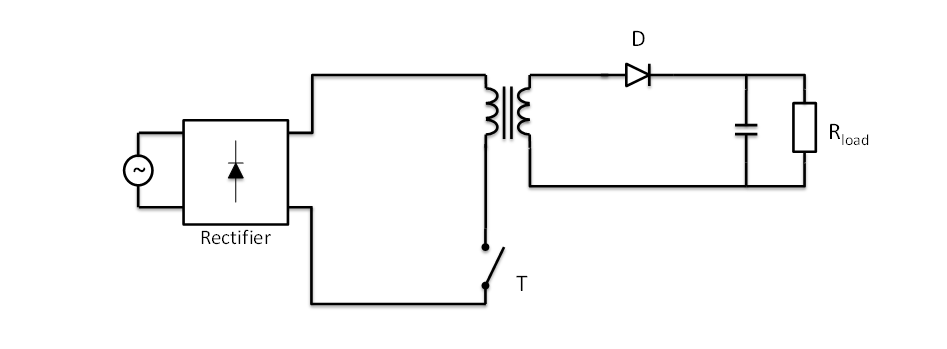
Cet exemple montre :

1. les équations permettant de calculer le rendement du dispositif
2. l’optimisation mono-objectif (minimisation de l’encombrement)
3. le post-processing du résultat d’optimisation
4. Optimisation pareto (encombrement vs. rendement)

Modélisation

L’objectif de la modélisation est de mettre en place les équations d’un convertisseur AC/DC en fonction de ses grandeurs caractéristiques (tensions d’entrée/sortie, puissance, rendement).

Le schéma du circuit est présentée en dessous. Le circuit de commande n’est pas pris en compte dans cet exemple.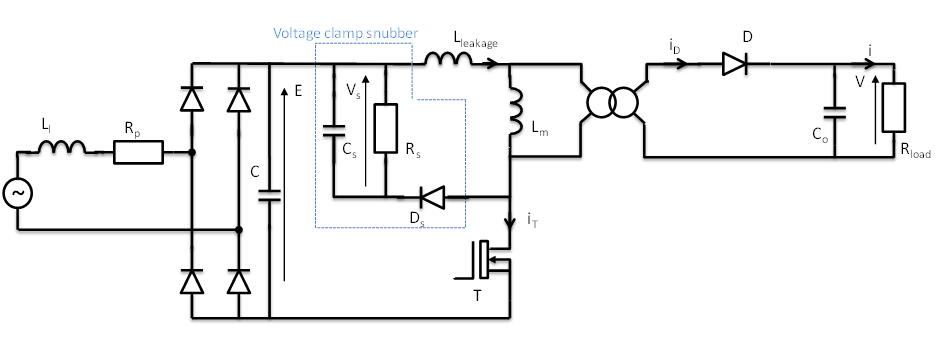

Les paramètres d’entrée

e	Entrefer du transformateur [m]
f	Fréquence de hachage [Hz]
m	Le rapport de transformation du transformateur [-]
Bmax	L’induction maximale dans le noyau du transformateur [T]
d1	Le diamètre du fil de l’enroulement primaire [mm2]
d2	Le diamètre du fil de l’enroulement secondaire[mm2]
delta1	Densité du courant dans l’enroulement primaire [A/m2]
delta2	Densité du courant dans l’enroulement secondaire[A/m2]
deltaV_percent	Distorsion admissible de la tension DC en sortie[%]
E	Tension de sortie du redresseur[V]
I	Courant en sortie[A]
k1	Coefficient de remplissage de l’enroulement primaire[-]
k2	Coefficient de remplissage de l’enroulement secondaire[-]
RD_on	Résistance de la diode[ohm]
RT_on	La résistance dynamique du transistor[ohm]
toff	Décalage d’ouverture du transistor [s]
V	Tension de sortie [V]
VD_reverse	Tension de la diode [V]
VT_peak	Tension admissible dans le transistor [V]
kp	Paramètre de calcul de pertes fer (formulation Steinmetz) [-]
xp	Paramètre de calcul de pertes fer (formulation Steinmetz) [-]
yp	Paramètre de calcul de pertes fer (formulation Steinmetz) [-]

Les équations

       

/*
   Convertisseur Flyback
  
   Fichier flyback.sml

   Modele de dimensionnement d'un convertisseur flyback.
   Réferénces:
   Jean Paul FERRIEUX, François FOREST - Alimentations à découpage, 
   convertisseurs à résonance 3e édition, Dunod, Paris, 1999  ISBN 2100041371

   Chérif LAROUCI. Conception et optimisation de convertisseurs statiques 
   pour l’électronique de puissance. Application aux structures à absorption 
   sinusoïdale. Thèse INPG LEG soutenue le 13 mai 2002.

   Ludovic JOURDAN. Stratégie de pré dimensionnement de convertisseurs 
   statiques. Application à une alimentation 42V-14V réversible pour 
   l’automobile. Thèse UJF LEG soutenue le 15 juillet 2002.
*/

intern mu0;
mu0 = 4*pi*1e-7;

/*Ouput power*/
P = V*I;

/*Cyclic ratio*/
alpha = sqrt((2*Lm*V*I*f)/pow(E,2));
beta = alpha * (1.0 + E/(m*V));

/*Magnetizing inductance (at continuous & discontinuous conduction limit)*/
Lm = pow((E*m*V),2)/(2*f*P*pow((E+m*V),2));

/*Transistor data*/
IT = E*alpha/(Lm*f);
IT_rms = IT*sqrt(alpha/3);
IT_average = E*pow(alpha,2)/(2*Lm*f);
  
/*Diode data*/
ID = E*alpha*m/(Lm*f);
ID_rms = sqrt(pow(ID,2)*(beta-alpha)+(pow((pow(m,2)*V/Lm),2))*
  pow((beta-alpha),3)/(3*pow(f,2))-2*ID*pow(m,2)*V*pow((beta-alpha),2)/(2*Lm*f));
  
/*Diode max current*/
IDmax = ( (V*I/(E*V*m/((V*m)+E))) + (E*m*V/(((V*m)+E)*2*Lm*f)) ) * m;

/*Transformer data*/
Aen = Lm*IT/Bmax;
Sfn = IT_rms*k1/(delta1*1e6) + ID_rms*k2/(m*(delta2*1e6));
AeSf = Aen*Sfn;
transformer_volume = 3e11*AeSf + 2772.3;

/*Leakage inductance estimation*/
L_leakage = Lm * 0.03;

/*Windings*/
n1 = sqrt((Lm*e)/(mu0*Aen));
n2 = n1/m;

/*Copper areas*/
A1 = IT_rms/(delta1*1e6);
A2 = ID_rms/(delta2*1e6);

A_copper = n1*k1*A1 + n2*k2*A2;
A_copper2 = pi*n1*k1*(pow(d1,2))/4+2*pi*n2*k2*(pow(d2,2))/4;

/*Voltage Clamp Snubber*/
Vs = VT_peak - E;
Rs = 2*Vs*(Vs-V/m)/(f*L_leakage*pow(IT, 2.0));
Cs = 10/(Rs*f);
VCS_losses = pow(Vs, 2.0)/Rs;

/*Output voltage smooth capacitor*/
Co = I/(deltaV_percent*V*f);
Co_volume = 1872.0*Co*1e6 + 250.0; //(400V series : mm^3 , Co in uF)

/*Rectifier voltage smooth capacitor*/
intern delatE_percent;
delatE_percent = 2.0;
C = IT_rms/(delatE_percent*E*50.0);
C_volume =  1872.0*C*1e6 + 250.0; //(400V series : mm^3 , C in uF)

/*Transistor commutation losses*/
Commutation_losses = (E+(V/m)+Vs)*E*alpha*toff/(2*Lm);

/*Transistor conduction losses*/
Conduction_losses_T = RT_on*pow(IT_rms,2);

/*Diode conduction losses*/
Conduction_losses_D = VD_reverse*I + RD_on*pow(ID_rms,2);

/*Transformer core losses*/
Core_losses = Kp2*pow(f,xp2)*pow(Bmax,yp2)*transformer_volume*1e-6;

/*Energetic balance*/
P_losses = Core_losses + Commutation_losses + Conduction_losses_T + Conduction_losses_D + VCS_losses;

/*Efficiency*/
Efficiency = P / (P + P_losses);

/*Total Volume (cm3)*/
Volume = transformer_volume + Co_volume + C_volume;

L’optimisation

Le scénario d’optimisation est le suivant :

• Trouver la valeur optimale de :
• L’entrefer du transformateur (e)
• La fréquence de hachage (f)
• Le rapport de transformation (m)
• Tel que :
• Le rendement soit supérieur à 0.85 (Efficiency)
• Le courant dans la diode soit inférieur à 14.0A (IDmax)
• Le volume du transformateur soit minimal (transformer_volume)
• Pour une valeur imposée de toutes les autres variables d’entrée

Le cahier des charges

    

/*Les intervalles de libertés d’optimisation*/
e  - Interval = [2.0e-4..0.0015] - valeur initiale = 5.0e-4
m  - Interval = [1.0..10.0]      - valeur initiale = 1.0
f  - Interval = [25000..100000]  - valeur initiale = 50000

/*Les variables imposées*/
Bmax           - Fixe - valeur = 0.2
d1             - Fixe - valeur = 0.4
d2             - Fixe - valeur = 0.8 
delta1         - Fixe - valeur = 4.0
delta2         - Fixe - valeur = 4.0 
deltaV_percent - Fixe - valeur = 2.0
E              - Fixe - valeur = 325.0
I              - Fixe - valeur = 4.5
k1             - Fixe - valeur = 3.0
k2             - Fixe - valeur = 3.0
kp2            - Fixe - valeur = 0.035
RT_on          - Fixe - valeur = 4.0
toff           - Fixe - valeur = 3.2e-8
V              - Fixe - valeur = 20.0
VD_reverse     - Fixe - valeur = 0.8
VT_peak        - Fixe - valeur = 400.0
xp2            - Fixe - valeur = 1.1
yp2            - Fixe - valeur = 2.63
RD_on          - Fixe - valeur = 0.1

/*Les contraintes sur les sortie*/
transformer_volume - Minimize               - valuer = 3822.5 - weight = 1.0
Efficiency         - Interval = [0.85..1.0]
IDmax              - Interval = [0.0..14.0]

/*L'optimiseur*/
Optimizer = SQP
Optimizer.Precision     = 1.0E-5
Optimizer.Max Iteration = 100

Le résultat d’optimisation

    

/*Les valeurs d'entrée trouvées*/
e  - valeur initiale = 5.0e-4  - valeur trouvée = 5.0e-4
f  - valeur initiale = 1.0     - valeur trouvée = 2.67
m  - valeur initiale = 45e5    - valeur trouvée = 18.5e6

/*Les valeurs de sorties trouvées*/
transformer_volume - valeur = 4295.19 (Minimisée) 
Efficiency         - valeur = 0.85 (limite min)
IDmax              - valeur = 10.48

Le post-processing

Le post-processeur de Cades peut servir pour montrer l’évolution de la fonction objectif à travers d’itérations d’optimisation :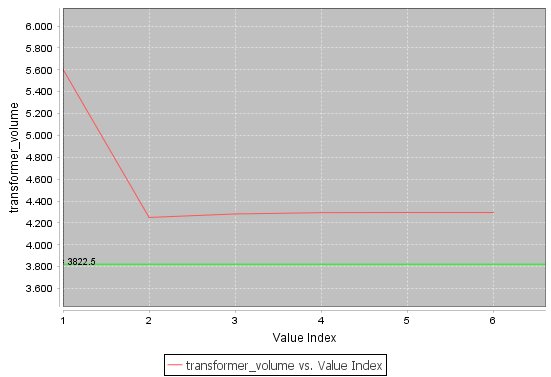

Optimisation pareto

Pour obtenir le front pareto (taransformer_volume vs. rendement), il faut utiliser le cahier des charges suivant:

    

/*Les intervales de libertés d’optimisation*/
e  - Interval = [2.0e-4..0.0015] - valuer initiale = 5.0e-4
m  - Interval = [1.0..10.0]      - valuer initiale = 1.0
f  - Interval = [25000..100000]  - valuer initiale = 50000

/*Les variables imposées*/
Bmax           - Fixe - valeur = 0.2
d1             - Fixe - valeur = 0.4
d2             - Fixe - valeur = 0.8 
delta1         - Fixe - valeur = 4.0
delta2         - Fixe - valeur = 4.0 
deltaV_percent - Fixe - valeur = 2.0
E              - Fixe - valeur = 325.0
I              - Fixe - valeur = 4.5
k1             - Fixe - valeur = 3.0
k2             - Fixe - valeur = 3.0
kp2            - Fixe - valeur = 0.035
RT_on          - Fixe - valeur = 4.0
toff           - Fixe - valeur = 3.2e-8
V              - Fixe - valeur = 20.0
VD_reverse     - Fixe - valeur = 0.8
VT_peak        - Fixe - valeur = 400.0
xp2            - Fixe - valeur = 1.1
yp2            - Fixe - valeur = 2.63
RD_on          - Fixe - valeur = 0.1

/*Les contraintes sur les sortie*/
transformer_volume - Minimize                - valuer = 3822.5 - weight = 1.0
Efficiency         - Maximize                - valuer = 1.0    - weight = 1.0
IDmax              - Interval = [0.0..14.0]

/*L'optimiseur*/
Optimizer = NSGA2

L’information du front pareto se trouve dans ce fichier des résultats. Il a l’allure suivante, montrant que pour des rendements supérieurs, il faut payer exponentiellement en volume:

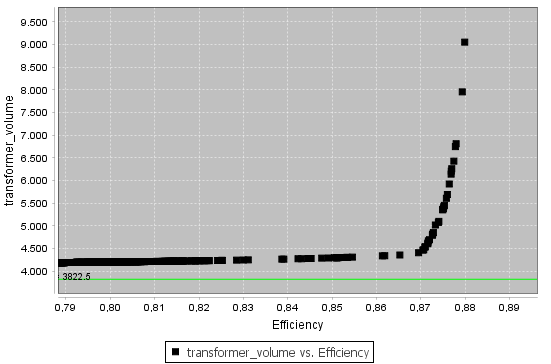
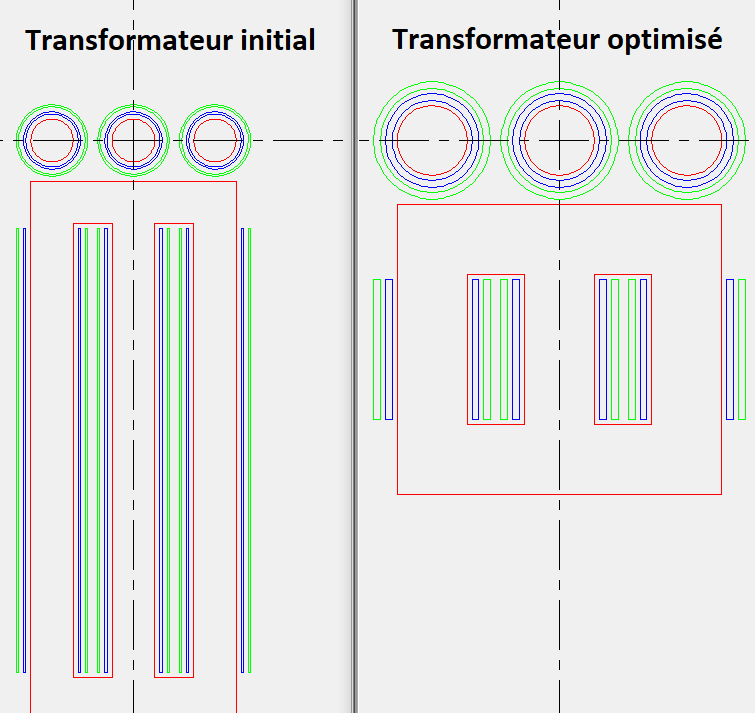
Transformateur de puissance

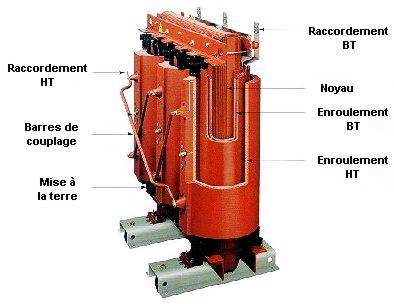
Cet exemple montre :

1. les équations permettant de calculer le coût total du dispositif
2. l’optimisation (minimisation du coût total)
3. le post-processing du résultat d’optimisation

Modélisation

L’objectif est de mettre en place un modèle électromagnétique pour dimensionner un transformateur en fonction de ses grandeurs caractéristiques (puissance, tensions, densité de courant, etc) ainsi que de définir un modèle économique permettant de prendre en compte le coût à l’achat (essentiellement matières premières) et le coût à l’utilisation (essentiellement les pertes).

---

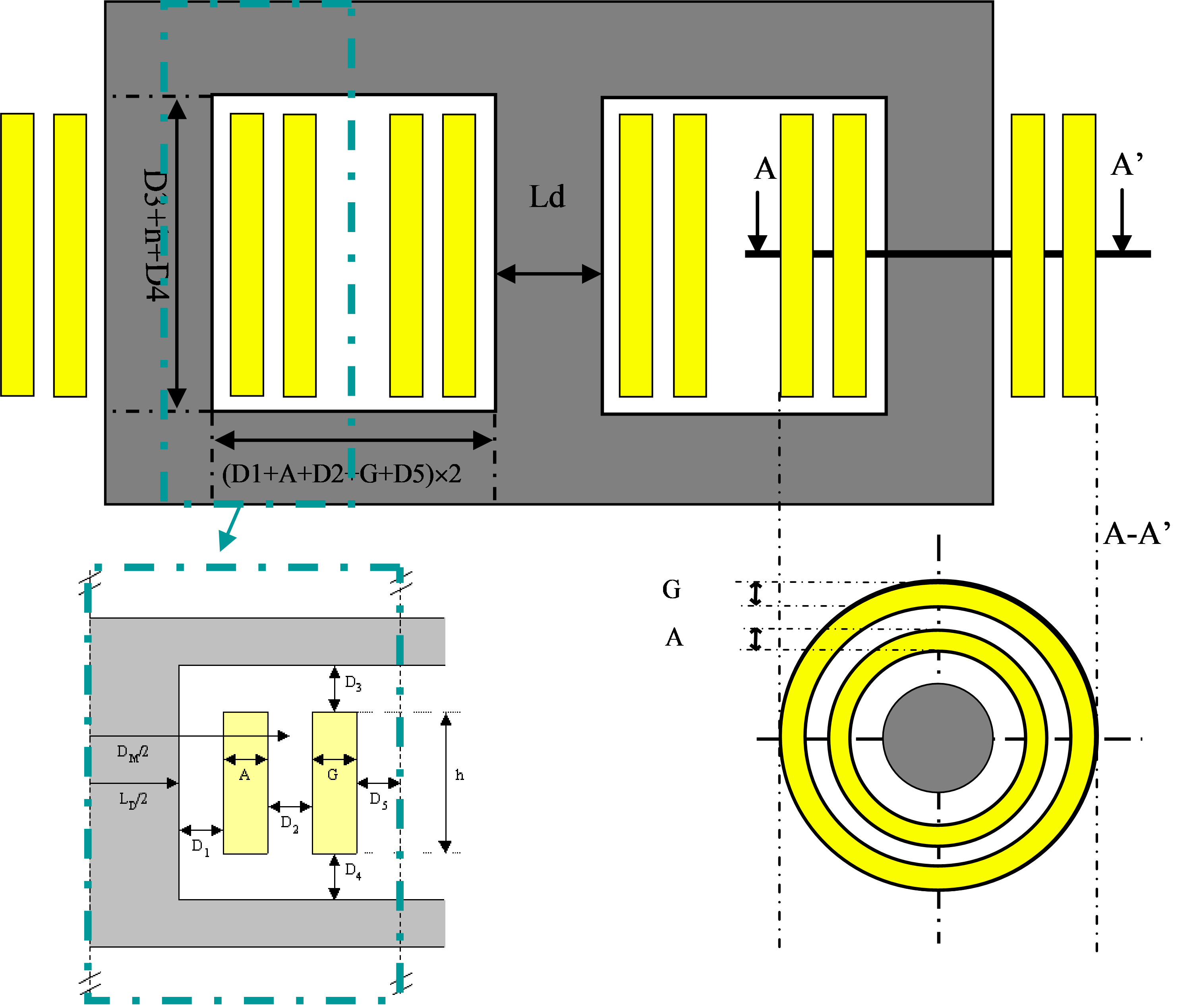
Les paramètres d’entrée

bt	Induction dans le matériau ferromagnétique
f	La fréquence de la tension d’alimentation
h	La hauteur d’une colonne
J	La densité du courant dans les conducteurs
N1	Le nombre de spires du circuit primaire
St	Puissance apparente totale
U1	Tension composée d’alimentation du circuit primaire

Les équations

       

/* 
   Transformateur
   
   Fichier transformateur.sml

   Modele de dimensionnement d'un transformateur triphase 3 colonnes

   Equations issues de:
   M. poloujadoff, R.D. Findlay, 
   " A PROCEDURE FOR ILLUSTRATING THE EFFECT OF VARIATION OF PARAMETERS 
     ON OPTIMAL TRANSFORMER DESIGN", IEEE Transactions on Power Systems,
   Vol. PWRS-1, No 4, November 1986 
*/

/* 
Definition de la loi donnant les pertes en watt/kg en fonction de l'induction pour les pertes fer 
*/
function pfkg(bt) = 1.996 - 8.125*bt + 12.277*bt*bt - 7.502*bt*bt*bt + 1.702*pow(bt,4);

/* Definition des constantes physiques */
muzero = 1.257e-006;

/* Definition de toutes les constantes du probleme */
D1 = 0.05;
D2 = 0.05;
D3 = 0.05;
D4 = 0.05;
D5 = 0.05;
DC = 8900;
DI = 7800;
FI = 0.8;
F1 = 0.7;
F2 = 0.7;
PC = 25;
PI = 12;
resistivite_cuivre = 2.6e-008;

/* 
Valeur actualise du cout de 1 watt de pertes cuivre en charge pendant 30 ans avec i=9% et 8760/5 heures et un prix de l'energie de 0.2778E-3 F/(watt*h). Donc pspc=0.2778E-3*somme(i=1 a 30,1/(1+0.09)^i)*3600*8760/5 car il y a 8760 heures dans l'annee et l'on considere les pertes joules moyennes consommees    sur une annee correspondent a un fonctionnement au regime nominal pendant le 1/5 eme de l'annee
*/
pspc = 5;
  
/* 
Valeur actualise du cout de 1 watt de pertes fer pendant 30 ans avec i=9% et 8760 heures et un prix de l'energie de 0.2778E-3 F/(watt*h). Donc pspc=0.2778E-3*somme(i=1 a 30,1/(1+0.09)^i)*3600*8760, car il y a 8760 heures dans l'annee
*/
pspf = 25;

/* Calcul de la puissance par colonne */
S = St/3.0;

/* Calcul de la tension simple par colonne a partir de la tension composee*/
V1 = U1/sqrt(3.0);

/* Calcul de la largeur des bobines primaires et secondaires */
A = (N1*S)/(V1*h*F1*J);
g = (N1*S)/(V1*h*F2*J);

/* Calcul du diametre moyen des bobines */
DM = ld + 2.0*D1 + 2.0*A + D2;

/* Largeur d'une colonne du transformateur */
ld = sqrt((2.0*sqrt(2.0)*V1)/(pow(pi, 2)*f*bt*N1*FI));

/* surface d'une colonne du diametre*/
AL = (pi/4.0)*pow(ld,2);

/* Calcul de l'inductance de fuite */
FF = (D2 + ((A + g)/3.0))/h;
X2 = muzero*pi*DM*pow(N1,2)*(2.0*pi*f)*FF;

/* Calcul de l'inductance de fuite P.U.*/
X2pu = X2/(pow(V1,2)/S);

/* Calcul du volume de fer */
Vol_fer0 = AL*FI*(8.0*(D1 + A + D2 + g + D5) + 6.0*ld + 3.0*(h + D4 + D3));

/* Calcul de la masse de fer */
Masse_fer0 = DI*Vol_fer0;

/* Calcul du cout du fer */
Prix_fer0 = PI*Masse_fer0;

/* Calcul du volume du cuivre */
Vol_cuivre0 = 3.0*pi*DM*h*(A*F1 + g*F2);

/* Calcul du cout du cuivre */
Prix_cuivre0 = PC*DC*Vol_cuivre0;

/* Calcul des pertes fer au Kilo: interpolation par les moindres carres */
Pertes_fer_Kg = pfkg(bt);

/* Calcul des pertes fer totales*/
Pertes_fer0 = Pertes_fer_Kg*Masse_fer0;

/* Calcul des pertes fers capitalisees */
Valeur_presente_pertes_fer = pspf*Pertes_fer0;

/* Calcul des pertes cuivres totales */
Pertes_cuivre0 = resistivite_cuivre*Vol_cuivre0*pow(J,2);

/* Calcul des pertes cuivres capitalisees*/
Valeur_presente_pertes_cuivre = pspc*Pertes_cuivre0;

/* Calcul de la longueur totale du transformateur */
ltt = 4*D5 + 3*(ld + 2*D1 + 2*g + 2*D2 + 2*A);

/* Calcul du prix total du transformateur*/
Prix_total_transfo = Prix_fer0 + Prix_cuivre0 + Valeur_presente_pertes_fer + Valeur_presente_pertes_cuivre;

L’optimisation

Le scénario d’optimisation est le suivant:

• Trouver la valeur optimale de :
• L’induction dans le matériau ferromagnétique (bt)
• La hauteur de la colonne (h)
• La densité du courant dans les conducteurs (J)
• Nombre de spires dans le circuit primaire (N1)
• Tel que :
• Le prix total du dispositif soit minimal (Prix_total_transfo)
• La réactance de fuite X2 soit comprise entre 5.76 et 8.64 avec une précision numérique relative de 1e-5
• Pour une valeur imposée de :
• La fréquence de la tension f = 50
• La puissance totale du dispositif St = 4*1e7
• La tension au primaire U1 = 60000

Le cahier des charges

    

/*Les intervales de libertés d’optimisation*/
bt - Interval = [0.5..1.9]   - valuer initiale = 1.7
f  - Fixe                    - valuer initiale = 50.0
h  - Interval = [1.0..1.4]   - valuer initiale = 4.432
J  - Interval = [50e4..45e5] - valuer initiale = 45e5
N1 - Interval = [100..1000]  - valuer initiale = 800
St - Fixe                    - valuer initiale = 4e7
U1 - Fixe                    - valuer initiale = 60000

/*Les contraintes sur les sortie*/
Prix_total_transfo - Minimize                - valuer = 1e6 - weight = 1.0
X2                 - Interval = [5.76..8.64]

/*L'optimiseur*/
Optimizer = SQP
Optimizer.Precision = 1.0E-5
Optimizer.Max Iteration = 100

Le résultat d’optimisation

    

/*Les valeurs d'entrée trouvées*/
bt - valeur initiale = 1.7   - valeur trouvée = 1.57
h  - valeur initiale = 4.432 - valeur trouvée = 1.4 (limite max)
J  - valeur initiale = 45e5  - valeur trouvée = 18.5e6
N1 - valeur initiale = 800   - valeur trouvée = 321.55

/*Les valeurs de sorties trouvées*/
Prix_total_transfo - valeur = 1.68e6 (Minimisée) 
X2                 - valeur = 8.64 (limite max)

Le post-processing

Le post-processeur de Cades peut servir pour montrer l’évolution de la fonction objectif à travers d’itérations d’optimisation :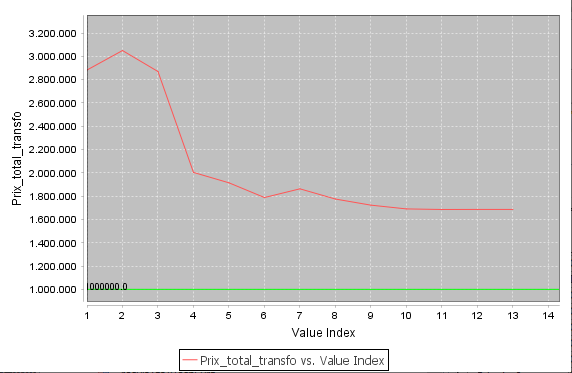

Il est aussi possible de créer et de visualiser la géométrie du dispositif à travers d’itérations :